题目内容
在△ABC中，若b2=ac，则cos（A-C）+cosB+cos2B的值是 ．
考点：正弦定理,两角和与差的余弦函数,二倍角的余弦
专题：计算题,三角函数的求值,解三角形
分析：由正弦定理可知，sin2B=sinAsinC，利用三角形的内角和，两角和与差的三角函数化简cos（A-C）+cosB+cos2B，然后利用二倍角公式化简即可．
解答：
解：∵b2=ac，
利用正弦定理可得sin2B=sinAsinC．
∴cos（A-C）+cosB+cos2B=cos（A-C）-cos（A+C）+cos2B
=2sinAsinC+cos2B=2sin2B+（1-2sin2B）=1．
故答案为：1．
利用正弦定理可得sin2B=sinAsinC．
∴cos（A-C）+cosB+cos2B=cos（A-C）-cos（A+C）+cos2B
=2sinAsinC+cos2B=2sin2B+（1-2sin2B）=1．
故答案为：1．
点评：本题考查三角函数的化简和正弦定理的运用，解题时要注意公式的合理选用，考查计算能力，属于中档题．
练习册系列答案
相关题目
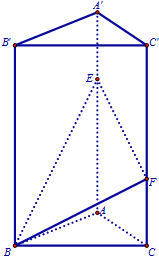已知三棱柱ABC-A′B′C′中，面BCC′B′⊥底面ABC，BB′⊥AC，底面ABC是边长为2的等边三角形，AA′=3，E，F分别在棱AA′，CC′上，且AE=C′F=2．
如图程序框图是计算22+42+…++1 0002的值，程序框图中条件语句中应填写