题目内容
已知△ABC中，角A，B，C的对边分别为a，b，c，若
=
，△ABC的外接圆半径为1．
（1）求角C的大小；
（2）求△ABC面积的最大值．
| sin2A-sin2C |
| sinB |
| a-b |
| 2 |
（1）求角C的大小；
（2）求△ABC面积的最大值．
考点：正弦定理,余弦定理
专题：解三角形
分析：（1）由已知得
=
，从而a2+b2-c2=ab，进而cosC=
=
=
，由此能求出∠C．
（2）由已知得c=（2R）sinC=2sin60°=
，由a2+b2≥2ab，即c2+ab≥2ab，得ab≤3．由此能求出△ABC面积的最大值．
| ||||
|
| a-b |
| 2 |
| a2+b2-c2 |
| 2ab |
| ab |
| 2ab |
| 1 |
| 2 |
（2）由已知得c=（2R）sinC=2sin60°=
| 3 |
解答：
解：（1）∵△ABC中，角A，B，C的对边分别为a，b，c，
=
，△ABC的外接圆半径为1，
∴
=
，
整理，得a2+b2-c2=ab，
∴cosC=
=
=
，
∴∠C=60°．
（2）∵△ABC的外接圆半径为R=1，∠C=60°，
∴c=（2R）sinC=2sin60°=
∵a2+b2≥2ab，即c2+ab≥2ab，
∴ab≤c2，即ab≤3．
故S△ABC=
absin 60°≤
×
=
．
∴△ABC面积的最大值为
．
| sin2A-sin2C |
| sinB |
| a-b |
| 2 |
∴
| ||||
|
| a-b |
| 2 |
整理，得a2+b2-c2=ab，
∴cosC=
| a2+b2-c2 |
| 2ab |
| ab |
| 2ab |
| 1 |
| 2 |
∴∠C=60°．
（2）∵△ABC的外接圆半径为R=1，∠C=60°，
∴c=（2R）sinC=2sin60°=
| 3 |
∵a2+b2≥2ab，即c2+ab≥2ab，
∴ab≤c2，即ab≤3．
故S△ABC=
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
3
| ||
| 4 |
∴△ABC面积的最大值为
3
| ||
| 4 |
点评：本题考查角的求法，考查三角形面积的最大值的求法，解题时要认真审题，注意正弦定理的合理运用．
练习册系列答案
相关题目
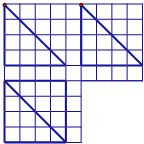如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图，则该多面体的外接球的体积为
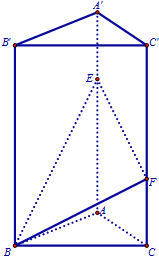已知三棱柱ABC-A′B′C′中，面BCC′B′⊥底面ABC，BB′⊥AC，底面ABC是边长为2的等边三角形，AA′=3，E，F分别在棱AA′，CC′上，且AE=C′F=2．
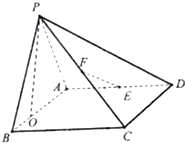如图，四棱锥P-ABCD的底面ABCD是矩形，平面PAB⊥平面ABCD，PA=AB=3，BC=2，E、F分别是棱AD，PC的中点