题目内容
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
函数f(x)=Asin(ωx+φ)(A>0,ω>0,-| π |
| 2 |
| 1 |
| 2 |
(1)求函数y=f(x)的解析式;
(2)将函数y=f(x)的图象向右平移
| π |
| 4 |
| π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)直接由图象求出A和T,由周期公式求得ω,利用五点作图的第一点求得φ,则函数解析式可求;
(2)由函数图象平移得到y=g(x),然后由x的范围求得函数值域.
(2)由函数图象平移得到y=g(x),然后由x的范围求得函数值域.
解答:
解:(1)由图可知,A=2,T=
-(-
)=π,
∴ω=2.
由五点作图的第一点知,2×(-
)+φ=0,解得φ=
.
∴f(x)=2sin(2x+
);
(2)将函数y=f(x)的图象向右平移
个单位,得到y=g(x)的图象的解析式为g(x)=2sin[2(x-
)+
]=2sin(2x-
).
由x∈(0,
),得2x-
∈(-
,
).
∴函数g(x)的值域为(-
,2].
| 11π |
| 12 |
| π |
| 12 |
∴ω=2.
由五点作图的第一点知,2×(-
| π |
| 12 |
| π |
| 6 |
∴f(x)=2sin(2x+
| π |
| 6 |
(2)将函数y=f(x)的图象向右平移
| π |
| 4 |
| π |
| 4 |
| π |
| 6 |
| π |
| 3 |
由x∈(0,
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴函数g(x)的值域为(-
| 3 |
点评:本题考查了y=Asin(ωx+φ)型函数的图象和性质,考查了三角函数图象的平移,是中档题.

练习册系列答案
相关题目
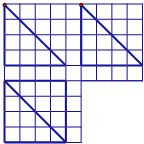 如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为
如图在边长为1的正方形网格中用粗线画出了某个多面体的三视图,则该多面体的外接球的体积为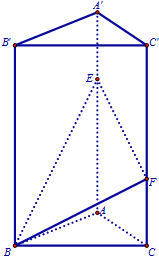 已知三棱柱ABC-A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.
已知三棱柱ABC-A′B′C′中,面BCC′B′⊥底面ABC,BB′⊥AC,底面ABC是边长为2的等边三角形,AA′=3,E,F分别在棱AA′,CC′上,且AE=C′F=2.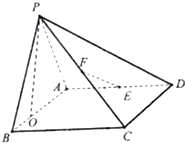 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,PA=AB=3,BC=2,E、F分别是棱AD,PC的中点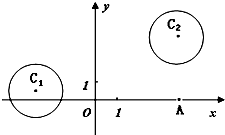 如图:已知圆C1:(x+3)2+(y-1)2=4与圆C2:(x-4)2+(y-5)2=4.
如图:已知圆C1:(x+3)2+(y-1)2=4与圆C2:(x-4)2+(y-5)2=4. 如图程序框图是计算22+42+…++1 0002的值,程序框图中条件语句中应填写
如图程序框图是计算22+42+…++1 0002的值,程序框图中条件语句中应填写