题目内容
已知椭圆C1:
+
=1与抛物线C2:y=x2-b
(1)若抛物线C2经过椭圆C1的焦点,且两曲线恰有三个不同的交点,求椭圆C1与抛物线C2的方程;
(2)当实数a,b满足什么关系式,椭圆C1与抛物线C2有四个不同的交点?并证明这四个交点共圆.
| x2 |
| a |
| y2 |
| 9 |
(1)若抛物线C2经过椭圆C1的焦点,且两曲线恰有三个不同的交点,求椭圆C1与抛物线C2的方程;
(2)当实数a,b满足什么关系式,椭圆C1与抛物线C2有四个不同的交点?并证明这四个交点共圆.
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)根据题意得出焦点为:F1(-
,0),F2(
,0),(0,-3)在抛物线上,可代入求解即可.
(2)得出椭圆C1与抛物线C2有四个不同的交点,
即a>b>3,利用圆内接四边形的性质证明即可.
| a-9 |
| a-9 |
(2)得出椭圆C1与抛物线C2有四个不同的交点,
|
解答:
解:(1)抛物线C2:y=x2-b,椭圆C1:
+
=1,
∵抛物线C2经过椭圆C1的焦点,且两曲线恰有三个不同的交点,
∴可判断:焦点为:F1(-
,0),F2(
,0),(0,-3)在抛物线上,
∴-3=0-b,
即b=3,
(
)2-3=0,a=12,
∴椭圆C1
+
=1,抛物线C2的方程为:y=x2-3,
(2)∵椭圆C1与抛物线C2有四个不同的交点,
∴
即a>b>3,
当a>b>3时,椭圆C1与抛物线C2有四个不同的交点,
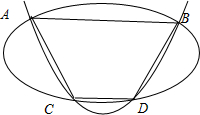
根据对称性可知,四边形ABDC为等腰梯形,
AB∥CD,
∴∠A+∠C=180°,
∠A=∠B,∠C=∠D,
∴∠A+∠D=180°,
对角互补
∴四边形ABDC为圆内接四边形,
∴A,B,C,D四点共圆.
| x2 |
| a |
| y2 |
| 9 |
∵抛物线C2经过椭圆C1的焦点,且两曲线恰有三个不同的交点,
∴可判断:焦点为:F1(-
| a-9 |
| a-9 |
∴-3=0-b,
即b=3,
(
| a-9 |
∴椭圆C1
| x2 |
| 12 |
| y2 |
| 9 |
(2)∵椭圆C1与抛物线C2有四个不同的交点,
∴
|
当a>b>3时,椭圆C1与抛物线C2有四个不同的交点,

根据对称性可知,四边形ABDC为等腰梯形,
AB∥CD,
∴∠A+∠C=180°,
∠A=∠B,∠C=∠D,
∴∠A+∠D=180°,
对角互补
∴四边形ABDC为圆内接四边形,
∴A,B,C,D四点共圆.
点评:本题综合考查了直线与圆锥曲线的位置关系,方程的求解与运用,属于综合题,难度较大.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
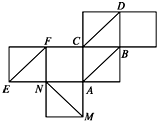 如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题:
如图为棱长是1的正方体的表面展开图,在原正方体中,给出下列三个命题: 如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…,以此类推,则第11行从左至右算第7个数字为
如图是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行;数字2,3出现在第2行,数字6,5,4(从左至右)出现在第3行;数字7,8,9,10出现在第4行;…,以此类推,则第11行从左至右算第7个数字为