题目内容
13.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x+4.(1)求y=f(x)的表达式;
(2)求直线y=2x+4与y=f(x)所围成的图形的面积.
分析 (1)设f(x)=ax2+bx+c,根据f′(x)=2x+2求出a、b的值,再由方程f(x)=0有两个相等的实根,△=0,求得c的值,即可得到函数的解析式.
(2)先由解方程组求出积分区间,再通过求定积分求出即可.
解答 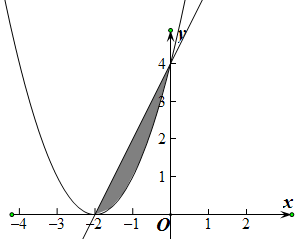 解:(1)设f(x)=ax2+bx+c,则f′(x)=2ax+b,又因为 f′(x)=2x+4,
解:(1)设f(x)=ax2+bx+c,则f′(x)=2ax+b,又因为 f′(x)=2x+4,
∴a=1,b=4,
∴f(x)=x2+4x+c.
由于方程f(x)=0有两个相等的实根,
∴△=16-4c=0,解得 c=4,∴f(x)=x2+4x+4.
(2)联立$\left\{\begin{array}{l}{y={x}^{2}+4x+4}\\{y=2x+4}\end{array}\right.$,解得x=-2或x=0,
即直线y=2x+4与y=f(x)所围成的图形的面积S=${∫}_{-2}^{0}$[2x+4-(x2+4x+4)]dx
=${∫}_{-2}^{0}$(-x2-2x)dx=(-$\frac{1}{3}{x}^{3}$-x2)|${\;}_{-2}^{0}$=-(-$\frac{8}{3}$-4)=$\frac{20}{3}$
点评 本题主要考查用待定系数法求函数的解析式,导数的运算,定积分的应用,属于中档题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
13.若变量x、y满足约束条件$\left\{\begin{array}{l}{3x+2y≤12}\\{x+2y≤8}\\{x≥0}\\{y≥0}\end{array}\right.$,则z=3x+4y的最大值是( )
| A. | 12 | B. | 14 | C. | 16 | D. | 18 |
1.已知z=($\frac{1+i}{1-i}$)8,则$\overline{z}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
8.以圆C1:x2+y2+4x+1=0与圆C2:x2+y2+2x+2y+1=0的公共弦为直径的圆的方程为( )
| A. | (x-1)2+(y-1)2=1 | B. | (x-$\frac{3}{5}$)2+(y-$\frac{3}{5}$)2=2 | C. | (x+1)2+(y+1)2=1 | D. | (x+$\frac{3}{5}$)2+(y+$\frac{3}{5}$)2=2 |