题目内容
已知抛物线C:y2=2px(p>0)的焦点为F,点P(a,a)(a>0)在抛物线上,且|PF|=
.
(1)求抛物线C的方程;
(2)设直线y=kx+b与抛物线交于A,B两点.
①当k=1,b=-4时,求证:点H(2,0)为△PAB的垂心;
②若△PAB的垂心为点H(m,0)(m>1),试求b的取值范围.
| 5 |
| 4 |
(1)求抛物线C的方程;
(2)设直线y=kx+b与抛物线交于A,B两点.
①当k=1,b=-4时,求证:点H(2,0)为△PAB的垂心;
②若△PAB的垂心为点H(m,0)(m>1),试求b的取值范围.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用点P(a,a)(a>0)在抛物线上,且|PF|=
,建立方程,求出p,即可求抛物线C的方程;
(2)①y=x-4代入y2=x,利用韦达定理,计算AB,PH的斜率,证明kAB•kPH=-1即可;
②y=kx+b代入y2=x,计算AB,PH的斜率,利用kAB•kPH=-1,即可求b的取值范围.
| 5 |
| 4 |
(2)①y=x-4代入y2=x,利用韦达定理,计算AB,PH的斜率,证明kAB•kPH=-1即可;
②y=kx+b代入y2=x,计算AB,PH的斜率,利用kAB•kPH=-1,即可求b的取值范围.
解答:
(1)解:∵点P(a,a)(a>0)在抛物线上,且|PF|=
,
∴a2=2pa,a+
=
,∴p=
,
∴抛物线C的方程是y2=x;
(2)①证明:设A(x1,y1),B(x2,y2),则
y=x-4代入y2=x,可得x2-9x+16=0,
∴x1+x2=9,∴y1+y2=1
∴kAB=
=
=1,
∵P(1,1),H(2,0),
∴kPH=
=-1,∴kAB•kPH=-1;
②解:y=kx+b代入y2=x,可得k2x2+2kbx+b2=0,
∴x1+x2=-
,∴y1+y2=-b
∴kAB=
=
=-
,
∵P(1,1),H(m,0),∴kPH=
,
∵kAB•kPH=-1,∴(-
)•
=-1,
∴b=
∵m>1,∴b<0.
| 5 |
| 4 |
∴a2=2pa,a+
| p |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
∴抛物线C的方程是y2=x;
(2)①证明:设A(x1,y1),B(x2,y2),则
y=x-4代入y2=x,可得x2-9x+16=0,
∴x1+x2=9,∴y1+y2=1
∴kAB=
| y2-y1 |
| x2-x1 |
| 1 |
| y1+y2 |
∵P(1,1),H(2,0),
∴kPH=
| 1-0 |
| 1-2 |
②解:y=kx+b代入y2=x,可得k2x2+2kbx+b2=0,
∴x1+x2=-
| 2b |
| k |
∴kAB=
| y2-y1 |
| x2-x1 |
| 1 |
| y1+y2 |
| 1 |
| b |
∵P(1,1),H(m,0),∴kPH=
| 1 |
| 1-m |
∵kAB•kPH=-1,∴(-
| 1 |
| b |
| 1 |
| 1-m |
∴b=
| 1 |
| 1-m |
∵m>1,∴b<0.
点评:本题考查抛物线的方程,考查直线与抛物线的位置关系,考查斜率的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
设f(x)=xex,若f′(xo)=0,则x0等于( )
| A、e2 | ||
| B、-1 | ||
C、
| ||
| D、ln2 |
下列不等式成立的是( )
| A、ex<x+1 | ||||
| B、lnx>x-1 | ||||
C、sinx<
| ||||
D、sinx>
|
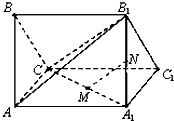 已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.
已知三棱柱ABC-A1B1C1,AA1⊥平面ABC,AB=AC=2,∠BAC=90°,四边形AA1C1C为正方形,M,N分别为A1C,A1B1中点.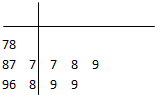 学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):
学校为测评班级学生对任课教师的满意度,采用“100分制”打分的方式来计分.现从某班学生中随机抽取10名,以下茎叶图记录了他们对某教师的满意度分数(以十位数字为茎,个位数字为叶):