题目内容
已知 A={（x，y）|-2≤x≤2，-2≤y≤2，x，y∈Z}，若点 P（x，y）∈A，则P满足|x|+|y|≤2的概率为 ．
考点：几何概型
专题：计算题,概率与统计
分析：在平面直角坐标系中画出集合A对应的平面区域及P满足条件的平面区域，分别求出平面区域内的整数坐标点的个数，利用个数比求概率．
解答：
解：集合A的元素为平面直角坐标系中正方形ABCD内的整数坐标点，共有25个；
满足条件|x|+|y|≤2的点在正方形EFGH内，共有9+4=13个，如图：
∴P满足|x|+|y|≤2的概率P=
．
故答案为：
．
满足条件|x|+|y|≤2的点在正方形EFGH内，共有9+4=13个，如图：
∴P满足|x|+|y|≤2的概率P=
| 13 |
| 25 |
故答案为：
| 13 |
| 25 |
点评：本题考查了古典概型的概率计算，分别求出平面区域内的整数坐标点的个数是关键．
练习册系列答案
相关题目
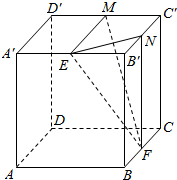在正方体ABCD-A′B′C′D′中，E，F，M，N分别是A′B′，BC，C′D′，B′C′的中点．