题目内容
已知关于x的二次函数 f(x)=x2+2ax+b2.
(I)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述函数图象与x轴有公共点的概率;
(Ⅱ)若a是从区间[0,3]内任取的一个实数,b是从区间[0,2]内任取的一个实数,求上述函数图象与x轴有公共点的概率.
(I)若a是从0,1,2,3四个数中任取的一个数,b是从0,1,2三个数中任取的一个数,求上述函数图象与x轴有公共点的概率;
(Ⅱ)若a是从区间[0,3]内任取的一个实数,b是从区间[0,2]内任取的一个实数,求上述函数图象与x轴有公共点的概率.
考点:几何概型,古典概型及其概率计算公式
专题:计算题,概率与统计
分析:(I)求出所取a,b的所有可能情况数,再求出满足条件函数图象与x轴有公共点的a,b情况数,利用个数比求概率;
(II)在平面直角坐标系中,画出以(a,b)为坐标的平面区域,利用符合条件的平面区域与所有区域的面积比求概率.
(II)在平面直角坐标系中,画出以(a,b)为坐标的平面区域,利用符合条件的平面区域与所有区域的面积比求概率.
解答:
解:(I)所取a,b的所有可能情况有4×3=12种情况;
∵函数图象与x轴有公共点,∴△=4a2-4b2≥0即a2≥b2,
∴满足条件的a,b有3+3+2+1=9种情况,
∴函数图象与x轴有公共点的概率为
=
;
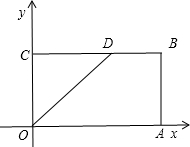
(II)如图△≥0所对应的区域为梯形OABD,
∴函数图象与x轴有公共点的概率P=
=
=
.
∵函数图象与x轴有公共点,∴△=4a2-4b2≥0即a2≥b2,
∴满足条件的a,b有3+3+2+1=9种情况,
∴函数图象与x轴有公共点的概率为
| 9 |
| 12 |
| 3 |
| 4 |
(II)如图△≥0所对应的区域为梯形OABD,
∴函数图象与x轴有公共点的概率P=
| S梯形OABD |
| S矩形OABC |
| ||
| 2×3 |
| 2 |
| 3 |

点评:本题考查了古典概型与几何概型的概率计算,利用基本事件个数比求古典概型的概率,利用实验事件所对应的平面区域的面积比求几何概型的概率.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
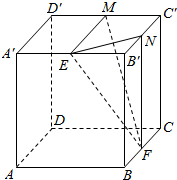 在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.
在正方体ABCD-A′B′C′D′中,E,F,M,N分别是A′B′,BC,C′D′,B′C′的中点.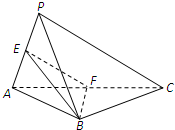 如图,在三棱锥P-ABC中,平面ABC⊥平面PAC,AB=BC,E,F分别是PA,AC的中点.求证:
如图,在三棱锥P-ABC中,平面ABC⊥平面PAC,AB=BC,E,F分别是PA,AC的中点.求证: