题目内容
为了检测某种产品的质量，抽取了一个容量为100的样本，数据的分组及频率如下表：
（1）求出上面频率分布表中的a，b，m，n的值；
（2）根据上表画出频率分布直方图；
（3）★根据上表和图，估计数据落在[10.95，11.35）范围内的频率是多少？
| 分组 | 频数 | 频率 |
| [10.75，10.85） | 3 | 0.03 |
| [10.85，10.95） | 9 | 0.09 |
| [10.95，11.05） | 13 | m |
| [11.05，11.15） | 16 | 0.16 |
| [11.15，11.25） | a | n |
| [11.25，11.35） | 20 | 0.20 |
| [11.35，11.45） | b | 0.07 |
| [11.45，11.55） | 4 | 0.04 |
| [11.55，11.65） | 2 | 0.02 |
| 合计 | 100 | 1.00 |
（2）根据上表画出频率分布直方图；
（3）★根据上表和图，估计数据落在[10.95，11.35）范围内的频率是多少？
考点：古典概型及其概率计算公式,频率分布直方图
专题：概率与统计
分析：（1）由已知中样本容量为100，结合频率=
，可求出b，m值，进而根据累积频率为1，累积频数为样本容量，可求出a，n值
（2）根据（1）中频率分布表，根据矩形高=
，求出各组数据在频率分布直方图中对应矩形的高，进而可得满足条件的频率分布直方图
（3）由上表可知数据落在[10.95，11.35）的有13+16+26+20=75个，进而可得可能性；
| 频数 |
| 样本容量 |
（2）根据（1）中频率分布表，根据矩形高=
| 频率 |
| 组距 |
（3）由上表可知数据落在[10.95，11.35）的有13+16+26+20=75个，进而可得可能性；
解答：
解：（1）∵样本容量为100，
∴m=
=0.13，n=1-（0.03+0.09+0.13+0.16+0.20+0.07+0.04+0.02）=0.26
a=0.26×100=26，
b=0.07×100=7，
（2）频率分布直方图如下图所示：
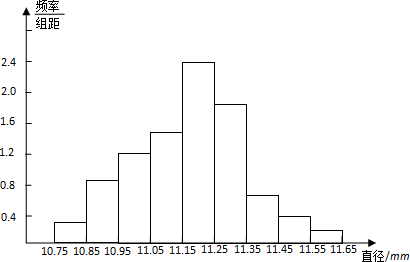
（3）由上表可知数据落在[10.95，11.35）的有13+16+26+20=75，
故数据落在[10.95，11.35）范围内的可能性是
=0.75
∴m=
| 13 |
| 100 |
a=0.26×100=26，
b=0.07×100=7，
（2）频率分布直方图如下图所示：
（3）由上表可知数据落在[10.95，11.35）的有13+16+26+20=75，
故数据落在[10.95，11.35）范围内的可能性是
| 75 |
| 100 |
点评：本题考查用样本的频率估计总体的分布，属基础题，熟练掌握频率=
，矩形高=
等常用公式是解答的关键．
| 频数 |
| 样本容量 |
| 频率 |
| 组距 |
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目