题目内容
己知函数f(x)=x,g(x)=ln(1+x)
(1)证明:当x>0时,恒有f(x)>g(x);
(2)当x>0时,不等式g(x)>
(k≥0)恒成立,求实数k的取值范围.
(1)证明:当x>0时,恒有f(x)>g(x);
(2)当x>0时,不等式g(x)>
| kx |
| k+x |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:计算题,作图题,导数的综合应用
分析:(1)令F(x)=f(x)-g(x)=x-ln(1+x);从而求导再判断单调性,从而证明;
(2)不等式g(x)>
可化为xln(1+x)>k(x-ln(1+x));从而得k<
;令F(x)=
,再作图象,从而利用图象解答.
(2)不等式g(x)>
| kx |
| k+x |
| xln(1+x) |
| x-ln(1+x) |
| xln(1+x) |
| x-ln(1+x) |
解答:
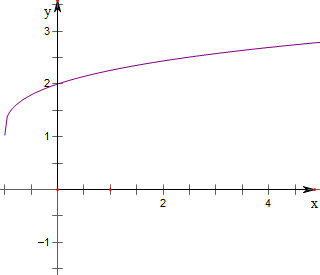 解:(1)证明:令F(x)=f(x)-g(x)=x-ln(1+x);
解:(1)证明:令F(x)=f(x)-g(x)=x-ln(1+x);
故F′(x)=1-
;
∵x>0,∴F′(x)>0;
故F(x)=f(x)-g(x)在(0,+∞)上是增函数,
故F(x)>F(0)=0,
故f(x)-g(x)>0,
即f(x)>g(x);
(2)不等式g(x)>
可化为
xln(1+x)>k(x-ln(1+x));
即k<
;
令F(x)=
,
作函数F(x)=
的图象如下,
故k≤2,
故0≤k≤2.
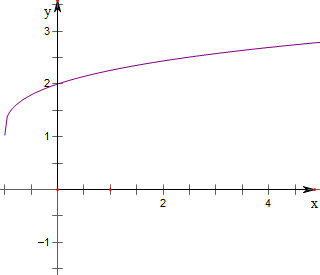 解:(1)证明:令F(x)=f(x)-g(x)=x-ln(1+x);
解:(1)证明:令F(x)=f(x)-g(x)=x-ln(1+x);故F′(x)=1-
| 1 |
| x+1 |
∵x>0,∴F′(x)>0;
故F(x)=f(x)-g(x)在(0,+∞)上是增函数,
故F(x)>F(0)=0,
故f(x)-g(x)>0,
即f(x)>g(x);
(2)不等式g(x)>
| kx |
| k+x |
xln(1+x)>k(x-ln(1+x));
即k<
| xln(1+x) |
| x-ln(1+x) |
令F(x)=
| xln(1+x) |
| x-ln(1+x) |
作函数F(x)=
| xln(1+x) |
| x-ln(1+x) |
故k≤2,
故0≤k≤2.
点评:本题考查了导数的综合应用及数形结合的数学思想应用,同时考查了恒成立问题,属于难题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
已知sinα=3cosα,则sin2α+3sinαcosα=( )
A、
| ||
| B、2 | ||
| C、3 | ||
| D、4 |
抛物线y=
x2的准线方程是( )
| 24 |
| 5 |
| A、y=1 | ||
B、y=-
| ||
| C、x=-1 | ||
| D、x=1 |
已知椭圆
+
=1上一点P到椭圆的一焦点的距离为3,则P到另一焦点的距离是( )
| x2 |
| 5 |
| y2 |
| 9 |
A、2
| ||
| B、2 | ||
| C、3 | ||
| D、6 |
如果三棱锥的每条侧棱和底面的边长都是a,那么这个三棱锥的外接球的体积是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|