题目内容
已知函数f(x)=
,g(x)=(
) ax2+bx(a≠0).若函数f(x)与g(x)的图象有且仅有两个公共点,坐标从左至右记为(x1,y1),(x2,y2),给出下列命题正确的是( )
|
| 1 |
| 2 |
| A、若a>0,则x1+x2<0,y1-y2>0 |
| B、若a<0,则x1+x2>0,y1-y2>0 |
| C、若a<0,则x1+x2<0,y1-y2符号无法确定 |
| D、若a<0,则x1+x2>0,y1-y2符号无法确定 |
考点:分段函数的应用
专题:
分析:画出函数的图象,利用函数的奇偶性,以及f(x)的对称性,即可得到结论.
解答:
解:作出函数f(x)的图象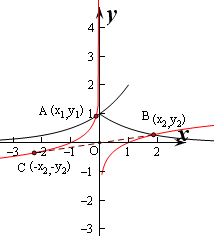 如图(红色曲线),
如图(红色曲线),
若a>0,二次函数y=ax2+bx先单调递减后单调递增,
则g(x)先单调递减,后单调递增,此时函数f(x)与g(x)的图象在x>0时不一定有交点,故此时无法判断.
若a<0,二次函数y=ax2+bx先单调递减,后单调递增则g(x)先单调递减后单调递增,
函数f(x)与g(x)的图象有且仅有两个公共点,有且仅有两个公共点A,B,
∵f(x)是奇函数,∴B(x2,y2),
关于原点对称的点C(-x2,-y2)在函数f(x)的图象上,
由图象可知A(x1,y1)高于C(-x2,-y2)点,
∴-x2<x1,-y2<y1,
即x1+x2>0,y1+y2>0,而y1-y2符号无法确定,
故选:D.
 如图(红色曲线),
如图(红色曲线),若a>0,二次函数y=ax2+bx先单调递减后单调递增,
则g(x)先单调递减,后单调递增,此时函数f(x)与g(x)的图象在x>0时不一定有交点,故此时无法判断.
若a<0,二次函数y=ax2+bx先单调递减,后单调递增则g(x)先单调递减后单调递增,
函数f(x)与g(x)的图象有且仅有两个公共点,有且仅有两个公共点A,B,
∵f(x)是奇函数,∴B(x2,y2),
关于原点对称的点C(-x2,-y2)在函数f(x)的图象上,
由图象可知A(x1,y1)高于C(-x2,-y2)点,
∴-x2<x1,-y2<y1,
即x1+x2>0,y1+y2>0,而y1-y2符号无法确定,
故选:D.
点评:本题主要考查函数和方程的应用,利用奇函数的对称性,以及数形结合是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
已知正△ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点P(x,y)是△ABC内部及其边界上一点,则
的最大值为( )
| y |
| x+1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
不等式2x2-3|x|-35>0的解集为( )
A、{x|x<-
| ||
B、{x|0<x<
| ||
| C、{x|x<5或x>7} | ||
| D、{x|x<-5或x>5} |
 蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第6幅图的蜂巢总数为( )
蜜蜂被认为是自然界中最杰出的建筑师,单个蜂巢可以近似地看作是一个正六边形,如图为一组蜂巢的截面图.其中第一个图有1个蜂巢,第二个图有7个蜂巢,第三个图有19个蜂巢,按此规律,第6幅图的蜂巢总数为( )| A、61 | B、90 | C、91 | D、127 |
不等式
≥0的解集是( )
| 1-2x |
| x+1 |
A、[-1,
| ||
B、(-1,
| ||
C、(-∞,-1)∪[
| ||
D、(-∞,-1]∪[
|
数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N)时,证明从n=k到n=k+1的过程中,相当于在假设成立的那个式子两边同乘以( )
| A、2k+2 | ||
| B、(2k+1)(2k+2) | ||
C、
| ||
D、
|