题目内容
正方体ABCD-A′B′C′D′中.M是AB的中点,则sin<
,
>= .
| DB′ |
| CM |
考点:异面直线及其所成的角
专题:空间角
分析:设棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出结果.
解答:
解: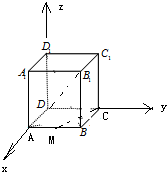 设棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,
设棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,
建立空间直角坐标系,
则D(0,0,0),B′(2,2,2),C(0,2,0),M(2,1,0),
∴
=(2,2,2),
=(2,-1,0),
cos<
,
>=
=
,
∴sin<
,
>=
=
.
故答案为:
.
 设棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,
设棱长为2,以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则D(0,0,0),B′(2,2,2),C(0,2,0),M(2,1,0),
∴
| DB′ |
| CM |
cos<
| DB′ |
| CM |
| 4-2 | ||||
|
| 1 | ||
|
∴sin<
| DB′ |
| CM |
1-(
|
| ||
| 15 |
故答案为:
| ||
| 15 |
点评:本题考查两向量的夹角的正弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
已知函数f(x)=
,g(x)=(
) ax2+bx(a≠0).若函数f(x)与g(x)的图象有且仅有两个公共点,坐标从左至右记为(x1,y1),(x2,y2),给出下列命题正确的是( )
|
| 1 |
| 2 |
| A、若a>0,则x1+x2<0,y1-y2>0 |
| B、若a<0,则x1+x2>0,y1-y2>0 |
| C、若a<0,则x1+x2<0,y1-y2符号无法确定 |
| D、若a<0,则x1+x2>0,y1-y2符号无法确定 |