题目内容
10.已知$f(x)=\left\{\begin{array}{l}1,x>0\\-1,x<0\end{array}\right.$,则不等式x+(x+2)f(x+2)≤5的解集是(-∞,-2)∪(2,$\frac{3}{2}$].分析 当x+2>0时,f(x+2)=1;x+2<0时,f(x+2)=-1,对x进行分类讨论后代入原不等式即可求出不等式的解集.
解答 解:∵不等式x+(x+2)f(x+2)≤5,
∴x+2+(x+2)f(x+2)≤7,
当x+2>0时,f(x+2)=1,代入原不等式得:x+2+x+2≤7⇒-2<x≤$\frac{3}{2}$;
当x+2<0时,f(x+2)=-1,代入原不等式得:x+2-x-2≤7⇒0≤7,即x<-2;
综上,原不等式的解集为(-∞,-2)∪(2,$\frac{3}{2}$].
故答案为:(-∞,-2)∪(2,$\frac{3}{2}$].
点评 此题考查了分段函数、不等式的解法,考查了分类讨论的数学思想,是一道基础题.

练习册系列答案
相关题目
18.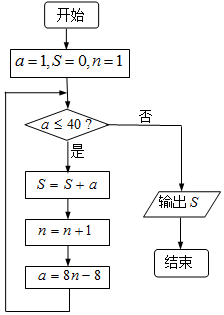 《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问
《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问
题的程序框图,若设每层外周枚数为a,则输出的结果为( )
 《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问
《孙子算经》是我国古代的数学著作,其卷下中有类似如下的问题:“今有方物一束,外周一匝有四十枚,问积几何?”如右图是解决该问题的程序框图,若设每层外周枚数为a,则输出的结果为( )
| A. | 81 | B. | 74 | C. | 121 | D. | 169 |
5.执行如图所示的程序框图,输出的n值为( )
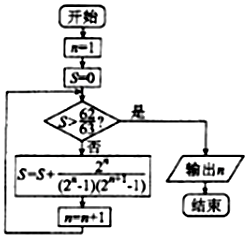

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
15.已知函数f(x)=a+$\sqrt{x}$lnx在(0,+∞)上有且仅有1个零点,则实数a的取值范围为( )
| A. | (-∞,0] | B. | (-∞,0]∪{$\frac{2}{e}$} | C. | (-∞,$\frac{2}{e}$) | D. | (-∞,$\frac{2}{e}$) |
2.若复数z满足(1+i)z=2i,其中i为虚数单位,则$\overline z$( )
| A. | 1-i | B. | 1+i | C. | 2-2i | D. | 2+2i |