题目内容

直线y=kx+1被曲线
x2
3
+
y2
4
=1截得的线段长度最大值是
 
．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：确定直线y=kx+1被曲线
x2
3
+
y2
4
=1截得的线段长度最大值是长轴长，即可得出结论．
解答： 解：曲线
x2
3
+
y2
4
=1的焦点坐标为（0，±1），直线y=kx+1过（0，1），
∴直线y=kx+1被曲线
x2
3
+
y2
4
=1截得的线段长度最大值是长轴长4．
故答案为：4．
点评：本题考查椭圆的性质，考查学生分析解决问题的能力，比较基础．
练习册系列答案
相关题目
某单位员工按年龄分为A，B，C三级，其人数之比为5：4：1，现用分层抽样的方法从总体中抽取一个容量为20的样本，已知C组中甲、乙二人均被抽到的概率是
1
25
，则该单位员工总数为
 
．
函数f（x）=sinx+
3
cosx（x∈[0，π]）的值域是
 
．
不等式
1-2x
x+1
＞1的解集是
 
．
设x、y满足约束条件
2x-y+2≥0
8x-y-4≤0
x≥0，y≥0
，若目标函数z=ax+by（a＞0，b＞0）的最大值为4，则
a+2b
ab
的最小值为
 
．
如图所示，A，B分别为椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左右顶点，以AB为一边做矩形ABCD，且AD=
3
b．P为椭圆在第一象限上的任意一点，连接PD，PC，分别与x轴交于点M，N，则
|MN|2
|AM||BN|
=（　　）
A、1
B、
4
3
C、
5
3
D、
3
下列函数中，既在（0，+∞）单调递增，又是偶函数的是（　　）
A、y=|x|+1
B、y=log2x
C、y=-x2+1
D、y=3x
函数f（x）=sinx•ln（x2+1）的部分图象可能是（　　）
A、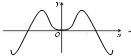
B、
C、
D、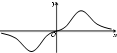
已知函数f（x）=3sinωx（ω＞0）在区间[-
π
3
，
π
4
]上的最大值是3，则ω的最小值为（　　）
A、
2
3
B、
3
2
C、2
D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网