题目内容
已知数列{an}的前n项和为Sn,a1=-
,
+Sn-1=-2(n≥2,n∈N*).
(1)求S1,S2,S3,S4的值;
(2)猜想Sn的表达式;并用数学归纳法加以证明.
| 1 |
| 2 |
| 1 |
| Sn |
(1)求S1,S2,S3,S4的值;
(2)猜想Sn的表达式;并用数学归纳法加以证明.
考点:数学归纳法
专题:点列、递归数列与数学归纳法
分析:(1)利用条件,代入计算,可求S1,S2,S3,S4的值;
(2)由(1)猜想Sn的表达式;利用数学归纳法的证明步骤进行证明.
(2)由(1)猜想Sn的表达式;利用数学归纳法的证明步骤进行证明.
解答:
解:(1)∵数列{an}的前n项和为Sn,a1=-
,
+Sn-1=-2(n≥2,n∈N*),
∴S1=-
,S2=-
,S3=-
,S4=-
.…(4分)(每个1分)
(2)猜想Sn=-
(n∈N*),…(6分)
数学归纳法证明:(1)当n=1时,S1=a1=-
,猜想成立;….(7分)
(2)假设n=k(k≥2,k∈N* )时猜想成立,即有:Sk=-
,
则n=k+1时,因为
=-Sk-2…(8分)
∴
=
-2=-
;…(10分)
从而有Sk+1=-
,即n=k+1时,猜想也成立;
由(1)(2)可知,Sn=-
(n∈N*),成立…(12分)
| 1 |
| 2 |
| 1 |
| Sn |
∴S1=-
| 1 |
| 2 |
| 2 |
| 3 |
| 3 |
| 4 |
| 4 |
| 5 |
(2)猜想Sn=-
| n |
| n+1 |
数学归纳法证明:(1)当n=1时,S1=a1=-
| 1 |
| 2 |
(2)假设n=k(k≥2,k∈N* )时猜想成立,即有:Sk=-
| k |
| k+1 |
则n=k+1时,因为
| 1 |
| Sk+1 |
∴
| 1 |
| Sk+1 |
| k |
| k+1 |
| k+2 |
| k+1 |
从而有Sk+1=-
| k+1 |
| k+2 |
由(1)(2)可知,Sn=-
| n |
| n+1 |
点评:本题考查数学归纳法,考查学生的计算能力,考查猜想与证明,正确理解数学归纳法的证明步骤是关键.

练习册系列答案
相关题目
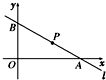 已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,则△ABO的面积的最小值为( )
已知直线l过点P(3,2),且与x轴、y轴的正半轴分别交于A,B两点,如图所示,则△ABO的面积的最小值为( )| A、6 | B、12 | C、24 | D、18 |
已知一个几何体的三视图如图所示,则这个几何体的体积是( )


A、
| ||
B、
| ||
C、
| ||
D、
|