题目内容
设函数f(x)=
sinxcosx+cos2x+a.
(Ⅰ)写出函数的最小正周期及单调递减区间;
(Ⅱ)当x∈[-
,
]时,函数f(x)的最大值与最小值的和为
,求f(x)的解析式.
| 3 |
(Ⅰ)写出函数的最小正周期及单调递减区间;
(Ⅱ)当x∈[-
| π |
| 6 |
| π |
| 3 |
| 3 |
| 2 |
考点:两角和与差的正弦函数,二倍角的正弦,二倍角的余弦,由y=Asin(ωx+φ)的部分图象确定其解析式,三角函数的最值
专题:三角函数的图像与性质
分析:(Ⅰ)化简可得f(x)=sin(2x+
)+a+
,易得周期,由2kπ+
≤2x+
≤2kπ+
解不等式可得单调区间;
(Ⅱ)由x∈[-
,
]可得-
≤sin(2x+
)≤1,进而由题意可得a的方程,解方程可得a值,可得解析式.
| π |
| 6 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
(Ⅱ)由x∈[-
| π |
| 6 |
| π |
| 3 |
| 1 |
| 2 |
| π |
| 6 |
解答:
解:(Ⅰ)化简可得f(x)=
sinxcosx+cos2x+a
=
sin2x+
+a=sin(2x+
)+a+
,
∴函数的最小正周期T=
=π,
由2kπ+
≤2x+
≤2kπ+
可得kπ+
≤x≤kπ+
,
∴函数的单调递减区间为[kπ+
,kπ+
](k∈Z);
(Ⅱ)∵x∈[-
,
],∴-
≤2x+
≤
,
∴-
≤sin(2x+
)≤1,
∴函数f(x)的最大值与最小值的和为(1+a+
)+(-
+a+
)=
,解得a=0
∴f(x)的解析式为:f(x)=sin(2x+
)+
| 3 |
=
| ||
| 2 |
| 1+cos2x |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
∴函数的最小正周期T=
| 2π |
| 2 |
由2kπ+
| π |
| 2 |
| π |
| 6 |
| 3π |
| 2 |
| π |
| 6 |
| 2π |
| 3 |
∴函数的单调递减区间为[kπ+
| π |
| 6 |
| 2π |
| 3 |
(Ⅱ)∵x∈[-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴-
| 1 |
| 2 |
| π |
| 6 |
∴函数f(x)的最大值与最小值的和为(1+a+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴f(x)的解析式为:f(x)=sin(2x+
| π |
| 6 |
| 1 |
| 2 |
点评:本题考查三角函数的公式,涉及三角函数的单调性和最值,属基础题.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
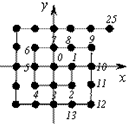 如图,将平面直角坐标系中的格点(横、纵坐标均为整 数的点)按如 下规则标上数字标签:原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2012×2013对应的格点的坐标 为( )
如图,将平面直角坐标系中的格点(横、纵坐标均为整 数的点)按如 下规则标上数字标签:原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2012×2013对应的格点的坐标 为( )| A、(-1006,1006) |
| B、(1005,-1006) |
| C、(1005,1006) |
| D、(1006,1006) |
下列周期为
的函数为( )
| π |
| 2 |
A、y=sin(2x+
| ||
B、y=2tan(x+
| ||
| C、y=cos3x | ||
| D、y=tan2x |