题目内容
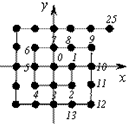 如图,将平面直角坐标系中的格点(横、纵坐标均为整 数的点)按如 下规则标上数字标签:原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2012×2013对应的格点的坐标 为( )
如图,将平面直角坐标系中的格点(横、纵坐标均为整 数的点)按如 下规则标上数字标签:原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2012×2013对应的格点的坐标 为( )| A、(-1006,1006) |
| B、(1005,-1006) |
| C、(1005,1006) |
| D、(1006,1006) |
考点:归纳推理
专题:计算题,推理和证明
分析:根据数据,归纳出点(-n,n)处标2n×(2n+1),即可得到结论.
解答:
解:观察已知中点(-1,1)处标6,即2×3,
点(-2,2)处标20,即4×5,
点(-3,3)处标42,即6×7,
…
由此推断
点(-n,n)处标2n×(2n+1),
∵2n=2012时,n=1006
故标签2012×2013对应的格点的坐标为(-1006,1006)
故选:A.
点(-2,2)处标20,即4×5,
点(-3,3)处标42,即6×7,
…
由此推断
点(-n,n)处标2n×(2n+1),
∵2n=2012时,n=1006
故标签2012×2013对应的格点的坐标为(-1006,1006)
故选:A.
点评:本题考查数列知识的运用,根据已知平面直角坐标系的格点(横、纵坐标均为整数的点)的规则,找出表上数字标签所示的规律,是解答的关键.

练习册系列答案
相关题目
北京奥运吉祥物由5个不同的“福娃”组成,将它们在展示台上随意摆放成一列,则不同的摆放顺序有( )
| A、1种 | B、5种 |
| C、60种 | D、120种 |
等差数列{an}的公差为d,则数列{3an}是( )
| A、非等差数列 | ||
| B、公差为d的等差数列 | ||
C、公差为
| ||
| D、公差为3d的等差数列 |
已知等差数列{an}的前n项和为Sn,且S4=S11,则a8为( )
| A、正数 | B、零 | C、负数 | D、不确定 |
已知直线l上两点A(-4,1),B(x,-3),且直线l的倾斜角为135°,则x的值是( )
| A、-8 | B、-4 | C、0 | D、8 |
已知直线y=kx+2和椭圆2x2+3y2=6有两个公共点,则k的取值范围( )
A、k<-
| ||||||||
B、-
| ||||||||
C、k≤-
| ||||||||
D、-
|
方程sinx=
在[
,
]上有解,则实数t的取值范围( )
| t |
| 2 |
| π |
| 2 |
| 5π |
| 4 |
A、[-
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
在三角形ABC中,
=
,
=
,则
=( )
| BC |
| a |
| CA |
| b |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|