题目内容
求y=sin3x+sinx3的导数.
考点:导数的运算
专题:导数的概念及应用
分析:直接由简单的复合函数的求导法则及基本初等函数的导数公式计算.
解答:
解:∵y=sin3x+sinx3,
∴y′=3sin2xcosx+3x2cosx3.
∴y′=3sin2xcosx+3x2cosx3.
点评:本题考查了导数的运算,考查了简单的复合函数的求导法则及基本初等函数的导数公式,是基础题.

练习册系列答案
相关题目
已知函数f(x)=sin(x-φ)-1(0<φ<
),且
(f(x)+1)dx=0,则函数f(x)的一个零点是( )
| π |
| 2 |
| ∫ |
0 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设l、m是两条不同的直线,α,β是两个不同的平面,则下列命题为真命题的是( )
| A、若m∥l,m∥α,则l∥α |
| B、若m⊥α,l⊥m,则l∥α |
| C、若α∥β,l⊥α,m∥β,则l⊥m |
| D、若m?α,m∥β,l?β,l∥α,则α∥β |
已知函数f(x)=ex-x2+8x,则在下列区间中f(x)必有零点的是( )
| A、(-2,-1) |
| B、(-1,0) |
| C、(0,1) |
| D、(1,2) |
若θ∈[0,
],sin2θ=
,则cosθ=( )
| π |
| 4 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
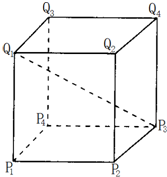 若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,
若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1,