题目内容
16.已知x>3,求f(x)=x+$\frac{4}{x-3}$的最小值.分析 利用基本不等式直接求解表达式的最小值即可.
解答 解:∵x>3,
∴x-3>0,
∴f(x)=x+$\frac{4}{x-3}$=x-3+$\frac{4}{x-3}$+3≥2$\sqrt{(x-3)•\frac{4}{x-3}}$+3=4+3=7,当且仅当x=5时取等号,
∴f(x)=x+$\frac{4}{x-3}$的最小值为7.
点评 本题考查基本不等式在最值中的应用,考查转化思想以及计算能力,注意表达式的变形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.阅读如图所示的程序框图,运行相应的程序.若输出的S为$\frac{25}{24}$,则判断框中填写的内容可以是( )
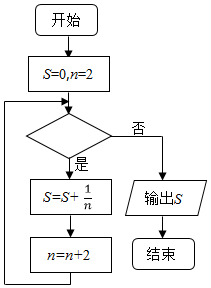

| A. | n=6 | B. | n<6 | C. | n≤6 | D. | n≤8 |
4.已知曲线f(x)=ke-2x在点x=0处的切线与直线x-y-1=0垂直,若x1,x2是函数g(x)=f(x)-|1nx|的两个零点,则( )
| A. | 1<x1x2<$\sqrt{e}$ | B. | $\frac{1}{\sqrt{e}}$<x1x2<1 | C. | 2<x1x2<2$\sqrt{e}$ | D. | $\frac{2}{\sqrt{e}}$<x1x2<2 |
8.若二次函数ax2+bx+c=0的两个实数根为-2,3(a<0),则ax2+bx+c>0的解集为( )
| A. | {x|x<-2或x>3} | B. | {x|x<-3或x>2} | C. | {x|-2<x<3} | D. | {x|-3<x<2} |
5.设函数f(x)=$\frac{x-a}{x-1}$,集合M={x|f(x)<0},P={x|f′(x)>0},若M?P,则实数a的取值范围是( )
| A. | (-∞,1) | B. | (0,1) | C. | (1,+∞) | D. | [1,+∞) |