题目内容
1．设a=logn（n+1），b=log（n+1）（n+2），n∈N*，则a，b的大小关系为b＜a．分析 化简$\frac{1}{a}$=log（n+1）n，从而利用做商法及基本不等式判断大小关系即可．
解答 解：∵n≥2，
∴a＞0，b＞0，
∴$\frac{1}{a}$=log（n+1）n，
∴$\frac{b}{a}$=log（n+1）n•log（n+1）（n+2）
＜（$\frac{lo{g}_{n+1}n+lo{g}_{n+1}（n+2）}{2}$）2＜1，
故b＜a，
故答案为：b＜a．
点评 本题考查了对数的运算及基本不等式的应用．
练习册系列答案
相关题目
9．
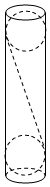如图所示，一个圆乒乓球筒，高为20厘米，底面半径为2厘米，球桶的上底和下底分别粘有一个乒乓球，乒乓球与球筒底面及侧面均相切（球筒和乒乓球厚度均忽略不计），一个平面与两个乒乓球均相切，且此平面截球筒边缘所得的图形为一个椭圆，则该椭圆的离心率为（ ）
如图所示，一个圆乒乓球筒，高为20厘米，底面半径为2厘米，球桶的上底和下底分别粘有一个乒乓球，乒乓球与球筒底面及侧面均相切（球筒和乒乓球厚度均忽略不计），一个平面与两个乒乓球均相切，且此平面截球筒边缘所得的图形为一个椭圆，则该椭圆的离心率为（ ）| A． | $\frac{1}{5}$ | B． | $\frac{\sqrt{15}}{4}$ | C． | $\frac{2\sqrt{6}}{5}$ | D． | $\frac{1}{4}$ |
13．设a，b∈R+，则下列不等式中一定不成立的是（ ）
| A． | a+b+$\frac{1}{\sqrt{ab}}$＞2$\sqrt{2}$ | B． | （a+b）（$\frac{1}{a}$+$\frac{1}{b}$）＞4 | ||
| C． | $\frac{{a}^{2}+{b}^{2}}{\sqrt{ab}}$＞ab | D． | $\frac{2ab}{a+b}$＞$\sqrt{ab}$ | ||
| E． | a+b+$\frac{1}{\sqrt{ab}}$＞2$\sqrt{2}$ | F． | $\frac{{a}^{2}+{b}^{2}}{\sqrt{ab}}$≥$\frac{2ab}{\sqrt{ab}}$=$2\sqrt{ab}$ |
10．若$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$不共线，则$\frac{1}{6}$$\overrightarrow{{e}_{1}}$-$\frac{1}{2}$$\overrightarrow{{e}_{2}}$与-2$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$（ ）
| A． | 一定共线 | B． | 一定不共线 | C． | 可能共线 | D． | 可能不共线 |
6．设等差数列{an}的前n项和为Sn，若数列{an}是单调递增数列，且满足a5≤6，S3≥9，则a6的取值范围是（ ）
| A． | （3，6] | B． | （3，6） | C． | [3，7] | D． | （3，7] |