题目内容
6.阅读如图所示的程序框图,运行相应的程序.若输出的S为$\frac{25}{24}$,则判断框中填写的内容可以是( )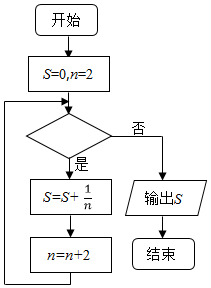
| A. | n=6 | B. | n<6 | C. | n≤6 | D. | n≤8 |
分析 模拟执行程序框图,依次写出每次循环得到的S,n的值,当n=10时,S=$\frac{25}{24}$,由题意,此时应该不满足条件,退出循环,输出S的值为$\frac{25}{24}$,故判断框中填写的内容可以是n≤8.
解答 解:模拟执行程序框图,可得
S=0,n=2
满足条件,S=$\frac{1}{2}$,n=4
满足条件,S=$\frac{1}{2}$+$\frac{1}{4}$=$\frac{3}{4}$,n=6
满足条件,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$=$\frac{11}{12}$,n=8
满足条件,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+$\frac{1}{8}$=$\frac{25}{24}$,n=10
由题意,此时应该不满足条件,退出循环,输出S的值为$\frac{25}{24}$,
故判断框中填写的内容可以是n≤8,
故选:D.
点评 本题主要考查了程序框图和算法,正确写出每次循环得到的S的值是解题的关键,属于基础题.

练习册系列答案
相关题目
16.将函数f(x)=$\sqrt{3}$cos(πx)图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位长度,得到函数g(x)的图象,则函数g(x)的单调区间是( )
| A. | [4k+1,4k+3](k∈Z) | B. | [2k+1,2k+3](k∈Z) | C. | [2k+1,2k+2](k∈Z) | D. | [2k-1,2k+2](k∈Z) |
17.某校高一、高二、高三年级学生人数分别是400,320,280.采用分层抽样的方法抽取50人,参加学校举行的社会主义核心价值观知识竞赛,则样本中高三年级的人数是( )
| A. | 20 | B. | 16 | C. | 15 | D. | 14 |
1.若函数y=2x上存在点(x,y)满足约束条件$\left\{\begin{array}{l}x+y-3≤0\\ x-2y-3≤0\\ x≥m\end{array}\right.$,则实数m的最大值为( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 2 |
15.若a,b是(0,2)内任意的两个实数,则使得函数f(x)=ln(ax2-2x+b)的值域为R的概率是( )
| A. | $\frac{1-ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{4}$ | D. | $\frac{1+2ln2}{4}$ |
