题目内容
若a=50.2，b=0.50.2，c=0.52，则a，b，c的大小关系为 ．
考点：幂函数的单调性、奇偶性及其应用
专题：计算题,函数的性质及应用
分析：由指数函数y=5x在R上递增，可得a＞1，再由指数函数y=0.5x在R上递减，可得c＜b＜1，即可得到大小关系．
解答：
解：由指数函数y=5x在R上递增，
则a=50.2＞50=1，
由指数函数y=0.5x在R上递减，
则由0＜0.2＜2，得1=0.50＞0.50.2＞0.52，
则有a＞b＞c．
故答案为：a＞b＞c．
则a=50.2＞50=1，
由指数函数y=0.5x在R上递减，
则由0＜0.2＜2，得1=0.50＞0.50.2＞0.52，
则有a＞b＞c．
故答案为：a＞b＞c．
点评：本题考查指数函数的性质和运用，考查指数函数的单调性应用于比较两数大小，考查运算能力，属于基础题．
练习册系列答案
金状元绩优好卷系列答案
相关题目
设全集为R，函数f（x）=ln
的定义域为M，则∁RM为（ ）
| 1+x |
| 1-x |
| A、（-1，1） |
| B、（-∞，-1）∪（1，+∞） |
| C、（-∞，-1]∪[1，+∞） |
| D、[-1，1] |
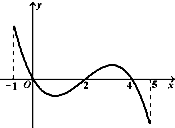已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示．下列关于f（x）的命题：