��Ŀ����
��֪������ƽ������
=��x��y������
�����������ʱ�뷽����ת�Ƚǵõ�����
=��xcos��-ysin�ȣ�xsin��+ycos�ȣ��������ѵ�B�Ƶ�A��ʱ�뷽����ת�ǵõ���P��
��1����֪ƽ���ڵ�A��1��2������B��1+
��2-2
�����ѵ�B�Ƶ�A����ʱ����ת
��õ���P�����P�����ꣻ
��2����ƽ����ֱ��l�ϵ�ÿһ��������ԭ������ʱ�뷽����ת
��õ��ĵ���ɵ�ֱ�߷�����l�䣺y=-
x+1����ԭ����ֱ��l���̣�
| AB |
| AB |
| AP |
��1����֪ƽ���ڵ�A��1��2������B��1+
| 2 |
| 2 |
| �� |
| 4 |
��2����ƽ����ֱ��l�ϵ�ÿһ��������ԭ������ʱ�뷽����ת
| �� |
| 4 |
| 3 |
���㣺���Ǻ����еĺ�ȱ任Ӧ��,ƽ������������������
ר�⣺ƽ��������Ӧ��,ֱ����Բ
��������1��ֱ�Ӹ�����Ŀ������⼴�ɣ�
��2����ֱ��l�ϵ�����һ��M��x��y������M������ԭ������ʱ�뷽����ת
��õ���N����
=��xcos
-ysin
��xsin
+ycos
��������ֱ�߷�����l�䣺y=-
x+1���������ֱ��l���̣�
��2����ֱ��l�ϵ�����һ��M��x��y������M������ԭ������ʱ�뷽����ת
| �� |
| 4 |
| ON |
| �� |
| 4 |
| �� |
| 4 |
| �� |
| 4 |
| �� |
| 4 |
| 3 |
���
�⣺��1���ߵ�A��1��2������B��1+
��2-2
����
��
=��
��-2
����
�ߵ�B�Ƶ�A����ʱ����ת
��õ���P
���������֪��
=(
cos
+2
sin
��
sin
-2
cos
)
=��3��-1����
���P��������3+1��-1+2��=��4��1����
��2����ֱ��l�ϵ�����һ��M��x��y����
��ת��ĵõ�
��
��
=��xcos
-ysin
��xsin
+ycos
��
=(
(x-y)��
(x+y))��
���N������Ϊ(
(x-y)��
(x+y))��
����ֱ�߷�����l�䣺y=-
x+1�ã�
(x+y)=-
•
(x-y)+1
�����y=(2+
)x-
��
| 2 |
| 2 |
��
| AB |
| 2 |
| 2 |
�ߵ�B�Ƶ�A����ʱ����ת
| �� |
| 4 |
���������֪��
| AP |
| 2 |
| �� |
| 4 |
| 2 |
| �� |
| 4 |
| 2 |
| �� |
| 4 |
| 2 |
| �� |
| 4 |
=��3��-1����
���P��������3+1��-1+2��=��4��1����
��2����ֱ��l�ϵ�����һ��M��x��y����
| OM |
| ON |
��
| ON |
| �� |
| 4 |
| �� |
| 4 |
| �� |
| 4 |
| �� |
| 4 |
=(
| ||
| 2 |
| ||
| 2 |
���N������Ϊ(
| ||
| 2 |
| ||
| 2 |
����ֱ�߷�����l�䣺y=-
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
�����y=(2+
| 3 |
| ||||
| 2 |
������������Ҫ�������������ʾ��Ӧ�ã��Լ����뷨��ֱ�߷��̣������е��⣮

��ϰ��ϵ�д�
�����Ŀ
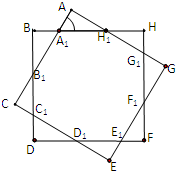 ��ͼ����ͼ����ʦҪ������ͬ���ĵı߳���Ϊ4�������κϳ�һ���˽���ͼ�Σ��ɶԳ��ԣ�ͼ��8�������ζ���ȫ�ȵ������Σ����AA1H1=����
��ͼ����ͼ����ʦҪ������ͬ���ĵı߳���Ϊ4�������κϳ�һ���˽���ͼ�Σ��ɶԳ��ԣ�ͼ��8�������ζ���ȫ�ȵ������Σ����AA1H1=����