题目内容
设数列{an}的前n项和为Sn,已知2Sn+1=Sn+4(n∈N*),a1=2
(1)证明:数列{an}是等比数列;
(2)设bn=an2,{bn}的前n项和为Tn,试比较
与3的大小;
(3)证明:不存在正整数n和大于4的正整数m使得等式am+1=
成立.
(1)证明:数列{an}是等比数列;
(2)设bn=an2,{bn}的前n项和为Tn,试比较
| Sn2 |
| Tn |
(3)证明:不存在正整数n和大于4的正整数m使得等式am+1=
| Sn+1-m |
| Sn-m |
考点:数列的求和,等比数列的性质
专题:等差数列与等比数列
分析:(1)将n换成n-1,两式相减得2an+1=an,求出a2,a3,运用等比数列的定义,即可证明;
(2)分别求出an,bn,Sn,Tn,令p=(
)n>0则
=3(-1+
),即可比较
与3的大小;
(3)运用反证法证明,求出am,得到Sn-m=
,运用(2)的结论,化简得到(4-m)2n=4+2m-1,对等式的左右两边分析,即可得证.
(2)分别求出an,bn,Sn,Tn,令p=(
| 1 |
| 2 |
| Sn2 |
| Tn |
| 2 |
| 1+p |
| Sn2 |
| Tn |
(3)运用反证法证明,求出am,得到Sn-m=
| an+1 |
| am |
解答:
(1)证明:∵2Sn+1=Sn+4,∴2Sn=Sn-1+4(n≥2),
相减得,2an+1=an,即
=
(n≥2),
由2S2=S1+4得a2=1,则a3=
,即
=
,
∴{an}是以2为首项,
为公比的等比数列;
(2)解:∵an=(
)n-2,Sn=
即Sn=4(1-(
)n),
bn=(
)n-2,Tn=
(1-(
)n),
令p=(
)n>0,
=
=3×
=3(-1+
)
当n→+∞时,p→0,
→3,
∴
<3;
(3)证明:若存在正整数n和大于4的正整数m使得等式am+1=
成立,
则am=
,∴am=
,Sn-m=
,4(1-(
)n)-m=(
)n+1-m
化简得(4-m)2n=4+2m-1,
则等式左边为负数,右边是正数,矛盾.
∴不存在正整数n和大于4的正整数m使得等式am+1=
成立.
相减得,2an+1=an,即
| an+1 |
| an |
| 1 |
| 2 |
由2S2=S1+4得a2=1,则a3=
| 1 |
| 2 |
| a2 |
| a1 |
| 1 |
| 2 |
∴{an}是以2为首项,
| 1 |
| 2 |
(2)解:∵an=(
| 1 |
| 2 |
2(1-(
| ||
1-
|
| 1 |
| 2 |
bn=(
| 1 |
| 4 |
| 16 |
| 3 |
| 1 |
| 4 |
令p=(
| 1 |
| 2 |
| Sn2 |
| Tn |
| 16(1-p)2 | ||
|
| 1-p |
| 1+p |
| 2 |
| 1+p |
当n→+∞时,p→0,
| Sn2 |
| Tn |
∴
| Sn2 |
| Tn |
(3)证明:若存在正整数n和大于4的正整数m使得等式am+1=
| Sn+1-m |
| Sn-m |
则am=
| Sn+1-m-Sn+m |
| Sn-m |
| an+1 |
| Sn-m |
| an+1 |
| am |
| 1 |
| 2 |
| 1 |
| 2 |
化简得(4-m)2n=4+2m-1,
则等式左边为负数,右边是正数,矛盾.
∴不存在正整数n和大于4的正整数m使得等式am+1=
| Sn+1-m |
| Sn-m |
点评:本题主要考查等比数列的通项和求和,注意运用an与Sn的关系式,同时考查反证法的运用,注意推出矛盾,本题属于中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
已知二面角α-l-β的大小为60°,异面直线m,n分别与α,β垂直,则m,n所成的角为( )
| A、120° | B、90° |
| C、60° | D、30° |
(
-
)n的展开式中只有第5项的二项式系数最大,则展开式中的常数项是( )
| 3 | x |
| 1 |
| x |
| A、28 | B、-28 |
| C、70 | D、-70 |
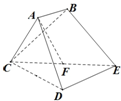 已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.
已知多面体ABCDE中,AB⊥面ACD,DE⊥面ACD,AC=AD=CD=DE=2,AB=1,F为CE的中点.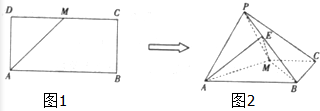 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=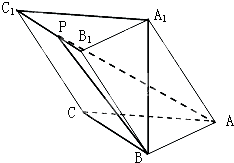 在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2
在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2