题目内容
17．已知抛物线y2=4x的焦点为F，过点F且倾斜角为45°的直线l与抛物线分别交于A、B两点，则|AB|=（ ）| A． | 3 | B． | 6 | C． | 8 | D． | 1 |
分析 写出直线方程代入抛物线方程利用韦达定理以及抛物线的性质，求解写出|AB|即可．
解答 解：直线的方程为y=x-1，代入y2=4x，整理得x2-6x+1=0，故x1+x2=6，
所以，|AB|=x1+x2+p=6+2=8．
故选：C．
点评 本题考查抛物线与直线的位置关系的应用，弦长公式的应用，抛物线的简单性质的应用，考查计算能力．
练习册系列答案
相关题目
5．
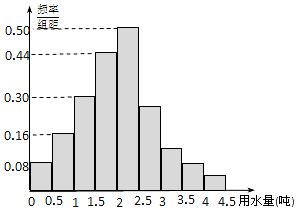某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：
（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？
某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：| 分组 | 频数 |
| [0，0.5） | 4 |
| [0.5，1） | 8 |
| [1，1.5） | 15 |
| [1.5，2） | 22 |
| [2，2.5） | 25 |
| [2.5，3） | 14 |
| [3，3.5） | 6 |
| [3.5，4） | 4 |
| [4，4.5） | 2 |
| 合计 | 100 |
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？
2．函数f（x）=$\frac{ln（4-x）}{x-2}$的定义域是（ ）
| A． | （-∞，4） | B． | （2，4） | C． | （0，2）∪（2，4） | D． | （-∞，2）∪（2，4） |
7．
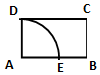如图，四边形ABCD为距形，AB=$\sqrt{3}$，BC=1，以A为圆心，AD为半径画圆，交线段AB于E，在圆弧DE上任取一点P，则直线AP与线段BC有公共点的概率为（ ）
如图，四边形ABCD为距形，AB=$\sqrt{3}$，BC=1，以A为圆心，AD为半径画圆，交线段AB于E，在圆弧DE上任取一点P，则直线AP与线段BC有公共点的概率为（ ）| A． | $\frac{\sqrt{3}π}{12}$ | B． | $\frac{12-\sqrt{3}π}{12}$ | C． | $\frac{1}{3}$ | D． | $\frac{2}{3}$ |