Question

14．已知正四棱柱ABCD-A₁B₁C₁D₁中，AA₁=2AB，则CD与平面BD D₁B₁所成角的等于45°．

Answer 1

分析 推导出BD⊥AC，DD₁⊥AC，从而AC⊥平面BD D₁B₁，进而∠CDO是CD与平面BD D₁B₁所成角，由此能求出CD与平面BD D₁B₁所成角．

解答 解：正四棱柱ABCD-A₁B₁C₁D₁中，设AA₁=2AB=2，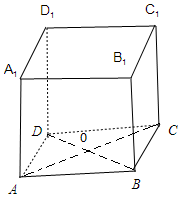
∴BD⊥AC，DD₁⊥AC，
∵BD∩DD₁=D，∴AC⊥平面BD D₁B₁，
∴∠CDO是CD与平面BD D₁B₁所成角，
∵四边形ABCD是正方形，∴∠CDO=45°，
∴CD与平面BD D₁B₁所成角是45°．
故答案为：45°．

点评 本题考查线面角的求法，涉及到空间中线线、线面、面面间的位置关系，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想，是中档题．