题目内容
已知函数f(x)=2x+2ax+b,且f(-1)=
,f(0)=2.
(Ⅰ)求函数f(x)的解析式并判断奇偶性;
(Ⅱ)若f(x)=
,求x的值.
| 5 |
| 2 |
(Ⅰ)求函数f(x)的解析式并判断奇偶性;
(Ⅱ)若f(x)=
| 65 |
| 8 |
考点:函数奇偶性的判断,函数解析式的求解及常用方法
专题:计算题,函数的性质及应用
分析:( I)由条件列出方程组,解出a,b,即可得到f(x)的解析式,再求定义域,计算f(-x),与f(x)比较,即可判断奇偶性;
(II)设2x=t(t>0),则有t+
=
,解出t,再运用指数函数的性质,即可得到x.
(II)设2x=t(t>0),则有t+
| 1 |
| t |
| 65 |
| 8 |
解答:
解:( I)已知得
解得:
,
则f(x)=2x+2-x.
显然函数f(x)的定义域为R,
由f(-x)=2-x+2x=f(x),
所以函数f(x)为偶函数;
(II)设2x=t(t>0),则有t+
=
,
即
=
,解得t=8或
,
即2x=8或
,
即有x=3或x=-3.
|
|
则f(x)=2x+2-x.
显然函数f(x)的定义域为R,
由f(-x)=2-x+2x=f(x),
所以函数f(x)为偶函数;
(II)设2x=t(t>0),则有t+
| 1 |
| t |
| 65 |
| 8 |
即
| t2+1 |
| t |
| 65 |
| 8 |
| 1 |
| 8 |
即2x=8或
| 1 |
| 8 |
即有x=3或x=-3.
点评:本题考查函数的奇偶性的判断和函数的解析式的求法,同时考查指数函数的性质,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
(0<φ<
)的图象如图,则( )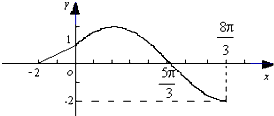
|
| π |
| 2 |

A、k=
| ||||||
B、k=
| ||||||
C、k=-
| ||||||
D、k=-2,ω=2,φ=
|
若点(16,2)在函数y=logax(a>0且a≠1)的图象上,则tan
的值为( )
| aπ |
| 3 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|