题目内容
 如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.
如图:内接于⊙O的△ABC的两条高线AD、BE相交于点H,过圆心O作OF⊥BC于 F,连接AF交OH于点G,并延长CO交圆于点I.(1)若
| OF |
| AH |
(2)若
| CH |
| OA |
| OB |
(3)若O为原点,点B的坐标为(-4,-3),点C的坐标为C(4,-3),试求点G的轨迹方程.
考点:轨迹方程
专题:综合题,平面向量及应用,直线与圆
分析:(1)先判断四边形AIBH为平行四边形,利用向量的线性运算,可求λ的值;
(2)利用利用向量的线性运算,结合平面向量基本定理,求x+y的值;
(3)利用代入法,可求点G的轨迹方程.
(2)利用利用向量的线性运算,结合平面向量基本定理,求x+y的值;
(3)利用代入法,可求点G的轨迹方程.
解答:
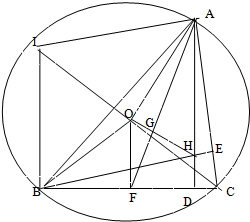 解:∵CI为直径,
解:∵CI为直径,
∴∠IAC和∠IBC均为直角,
∴AI∥BE,BI∥AD,
∴四边形AIBH为平行四边形
(1)
=
=
=λ
,∴λ=
;
(2)
=
+
=
+
而
=
-
=
-
∴
=
+
=
+
=
+
+
∴
=
+
而
=x
+y
,
∴x+y=2
(3)∵OF=
IB=
AH,∴FG=
GA又F为BC的中点,∴G为△ABC的重心
显然,A的轨迹为除B,C外的⊙O,其方程为:x2+y2=25(y≠-3)
设A(x0,yo),G(x,y),则
,得:
代入⊙O的方程并化简得G的轨迹方程为:x2+(y+2)2=
(y≠-3).
 解:∵CI为直径,
解:∵CI为直径,∴∠IAC和∠IBC均为直角,
∴AI∥BE,BI∥AD,
∴四边形AIBH为平行四边形
(1)
| OF |
| 1 |
| 2 |
| IB |
| 1 |
| 2 |
| AH |
| AH |
| 1 |
| 2 |
(2)
| OH |
| OB |
| BH |
| OB |
| IA |
而
| IA |
| OA |
| OI |
| OA |
| CO |
∴
| OH |
| OB |
| BH |
| OB |
| IA |
| OB |
| OA |
| OC |
∴
| CH |
| OA |
| OB |
| CH |
| OA |
| OB |
∴x+y=2
(3)∵OF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
显然,A的轨迹为除B,C外的⊙O,其方程为:x2+y2=25(y≠-3)
设A(x0,yo),G(x,y),则
|
|
代入⊙O的方程并化简得G的轨迹方程为:x2+(y+2)2=
| 25 |
| 9 |
点评:本题考查向量知识的运用,考查轨迹方程,考查代入法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
 如图,在△ABC中,G为中线AM的中点,O为△ABC外一点,若
如图,在△ABC中,G为中线AM的中点,O为△ABC外一点,若