题目内容

从10位学生中选出5人参加数学竞赛．
（1）甲必须选入的有多少种不同的选法？
（2）甲、乙、丙不能同时都入选的有多少种不同的选法？
考点：排列、组合及简单计数问题
专题：排列组合
分析：（1）学甲入选，再从剩下的9人选4，问题得以解决．
（2）利用间接法，先求出没有限制条件的，再排除甲、乙、丙同时都入选，问题得以解决
解答： 解：（1）学甲入选，再从剩下的9人选4，故甲必须选入的有C94=126种不同选法，
（2）没有限制条件的选择方法有C105=252种，甲、乙、丙同时都入选有C72=21种，
故甲、乙、丙不能同时都入选的有252-21=231．
点评：本题考查排列、组合的应用，是简单题，注意分类讨论、正确计算即可．
练习册系列答案
相关题目
已知{an}为等差数列，其前n项和为Sn，若a3=6，S3=12，则S12等于（　　）
A、288B、90
C、156D、126
已知极坐标的极点与平面直角坐标系的原点重合，极轴与x轴的正半轴重合，且长度单位相同，圆C的参数方程为
x=1+2cosα
y=
3
+2sinα
（α为参数），点Q的极坐标为（4，-
2π
3
）．
（Ⅰ）写出圆C的直角坐标方程和极坐标方程；
（Ⅱ）已知点P是圆C上的任意一点，求P，Q两点间距离的最小值．
如图，在四棱锥P-ABCD中，底面ABCD是矩形，侧棱PD⊥底面ABCD，PD=CD，AB=4，BC=3，E是PD的中点．
（1）证明：PB∥平面ACE
（2）若Q为直线PB上任意一点，求几何体Q-ACE的体积．
解不等式：x2-x-2＞0．
如图：内接于⊙O的△ABC的两条高线AD、BE相交于点H，过圆心O作OF⊥BC于 F，连接AF交OH于点G，并延长CO交圆于点I．
（1）若
OF
=λ
AH
，试求λ的值；
（2）若
CH
=x
OA
+y
OB
，试求x+y的值；
（3）若O为原点，点B的坐标为（-4，-3），点C的坐标为C（4，-3），试求点G的轨迹方程．
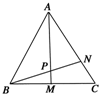如图所示，在△ABC中，点M是BC的中点，设
AB
=
a
，
AC
=
b
，点N在AC上，且AN=2NC，AM与BN相交于点P，AP=λAM，求
（1）λ的值；
（2）用
a
，
b
表示
AP
．
已知圆锥曲线E的两个焦点坐标是F1（-
2
，0），F2（
2
，0），且离心率为e=
2
；
（Ⅰ）求曲线E的方程；
（Ⅱ）设曲线E表示曲线E的y轴左边部分，若直线y=kx-1与曲线E相交于A，B两点，求k的取值范围；
（Ⅲ）在条件（Ⅱ）下，如果|
AB
|=6
3
，且曲线E上存在点C，使
OA
+
OB
=m
OC
，求m的值．
“解方程（
3
5
）x+（
4
5
）x=1”有如下思路：构造函数f（x）=（
3
5
）x+（
4
5
）x，易知f（x）在R上单调递减，且f（2）=1，故原方程有唯一解x=2，类比上述解题思路，不等式x6-（x+2）＞（x+2）3-x2的解集是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网