题目内容
6.如果ξ~B $({20,\frac{1}{3}})$,则使P(ξ=k)取最大值时的k值为( )| A. | 5或6 | B. | 6或7 | C. | 7或8 | D. | 以上均错 |
分析 随机变量ξ~B(20,$\frac{1}{3}$),当P(ξ=k)的表达式,由式子的意义知:概率最大也就是ξ最可能的取值.这和期望的意义接近.由Eξ=20×$\frac{1}{3}$=$\frac{20}{3}$,知k=6,或k=7都可能是极值,由此能求出p(ξ=k)取最大值时k的值.
解答 解:随机变量ξ~B(20,$\frac{1}{3}$),
∴当P(ξ=k)=${C}_{20}^{k}$($\frac{1}{3}$)20-k(1-$\frac{1}{3}$)k=($\frac{1}{3}$)20•2k•${C}_{20}^{k}$,
由式子的意义知:概率最大也就是ξ最可能的取值,这和期望的意义接近.
∵Eξ=20×$\frac{1}{3}$=$\frac{20}{3}$,
∴k=6,或k=7都可能是极值,
∵P(ξ=6)=P(ξ=7),
∴p(ξ=k)取最大值时k的值是6或7.
故选:B.
点评 本题考查二项分布的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
19.编号为1,2,3,4,5,6的六个人分别去坐编号为1,2,3,4,5,6的六个座位,其中有且只有两个人的编号与座位编号一致的坐法有( )
| A. | 135种 | B. | 90种 | C. | 150种 | D. | 15种 |
20.在等差数列中,am=n,an=m(m≠n),则am+n为( )
| A. | m-n | B. | 0 | C. | m2 | D. | n2 |
1.直线x=t分别与函数f(x)=ex+1的图象及g(x)=2x-1的图象相交于点A和点B,则|AB|的最小值为( )
| A. | 2 | B. | 3 | C. | 4-2ln2 | D. | 3-2ln2 |
18.设x,y满足约束条件$\left\{\begin{array}{l}{x+y-2≥0}\\{x-y+2≥0}\\{x≤2}\end{array}\right.$,则目标函数z=$\frac{y}{x+1}$的取值范围是( )
| A. | [-2,0] | B. | (-∞,-2]∪[0,+∞) | C. | [0,2] | D. | (-∞,0]∪[2,+∞) |
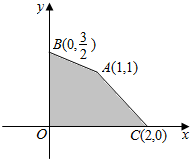 给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.