题目内容
14.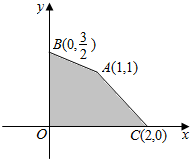 给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.
给出平面区域为图中四边形ABOC内部及其边界,目标函数为z=ax-y,若当且仅当x=1,y=1时,目标函数z取最小值,则实数a的取值范围是$-1<a<-\frac{1}{2}$.
分析 根据约束条件画出可行域,利用几何意义求最值,z=ax-y表示直线在y轴上的截距的相反数,a表示直线的斜率,只需求出a取值在什么范围时,直线z=ax-y在y轴上的截距最优解在点A处即可.
解答 解:由可行域可知,直线AC的斜率=$\frac{1-0}{1-2}$=-1,
直线AB的斜率=$\frac{1-\frac{3}{2}}{1-0}$=-$\frac{1}{2}$,
当直线z=ax-y的斜率介于AC与AB之间时,
A(1,1)是该目标函数z=ax-y的唯一最优解,
所以-1<a<-$\frac{1}{2}$
故答案为:$-1<a<-\frac{1}{2}$.
点评 本题主要考查了简单的线性规划,以及利用几何意义求最值的方法反求参数的范围,属于中档题.解答的关键是根据所给区域得到关于直线斜率的不等关系,这是数学中的数形结合的思想方法.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
7.在?ABCD中,已知$\overrightarrow{AC}$=(-4,2),$\overrightarrow{BD}$=(2,-6),那么|2$\overrightarrow{AB}$+$\overrightarrow{AD}$|=( )
| A. | 5$\sqrt{5}$ | B. | 2$\sqrt{5}$ | C. | 2$\sqrt{10}$ | D. | $\sqrt{85}$ |
8.函数f(x)=3sin($\frac{x}{4}$+$\frac{π}{6}$)(x∈R)的最小正周期( )
| A. | 2π | B. | 4π | C. | 8π | D. | π |
6.如果ξ~B $({20,\frac{1}{3}})$,则使P(ξ=k)取最大值时的k值为( )
| A. | 5或6 | B. | 6或7 | C. | 7或8 | D. | 以上均错 |