题目内容
20.在等差数列中,am=n,an=m(m≠n),则am+n为( )| A. | m-n | B. | 0 | C. | m2 | D. | n2 |
分析 可求得d=$\frac{{a}_{m}-{a}_{n}}{m-n}$=-1,从而求am+n的值.
解答 解:∵{an}是等差数列,
∴d=$\frac{{a}_{m}-{a}_{n}}{m-n}$=$\frac{n-m}{m-n}$=-1,
∴am+n=am+(m+n-m)d
=n-n=0,
故选B.
点评 本题考查了等差数列的性质的判断与应用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
8.函数f(x)=3sin($\frac{x}{4}$+$\frac{π}{6}$)(x∈R)的最小正周期( )
| A. | 2π | B. | 4π | C. | 8π | D. | π |
15.在平面直角坐标系xOy中,P(x,y)为不等式$\left\{\begin{array}{l}{x+2y≤4}\\{x-y≤3}\\{x≥1}\end{array}\right.$所表示的平面区域内的一个动点,则z=$\frac{y+1}{x+1}$的最大值为( )
| A. | $\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{3}{2}$ | D. | $\frac{3}{4}$ |
6.如果ξ~B $({20,\frac{1}{3}})$,则使P(ξ=k)取最大值时的k值为( )
| A. | 5或6 | B. | 6或7 | C. | 7或8 | D. | 以上均错 |
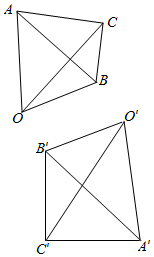 如图所示,有点O,O′和△A′B′C′,满足下列条件:$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{O{{\;}^{'}A}^{'}}$=-$\overrightarrow{a}$,$\overrightarrow{O{{\;}^{'}B}^{'}}$=-$\overrightarrow{b}$,O′C′=-$\overrightarrow{c}$,求证:△ABC≌△A′B′C′.
如图所示,有点O,O′和△A′B′C′,满足下列条件:$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,$\overrightarrow{O{{\;}^{'}A}^{'}}$=-$\overrightarrow{a}$,$\overrightarrow{O{{\;}^{'}B}^{'}}$=-$\overrightarrow{b}$,O′C′=-$\overrightarrow{c}$,求证:△ABC≌△A′B′C′.