题目内容
已知f(x)=x2-2|x|,则满足f[f(x)]=-
的实数x的个数为( )
| 1 |
| 2 |
| A、2 | B、4 | C、6 | D、8 |
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:令f(x)=t,现在来求满足f(t)=-
的t,容易判断f(t)为偶函数,所以可先求t≥0时的t,解出为t=1+
,或1-
.根据偶函数的对称性知,t<0时,满足f(t)=-
的解为-1-
,或-1+
,而接着就要判断以下几个方程:f(x)=1+
,f(x)=1-
,f(x)=-1-
,f(x)=-1+
解的个数,由于f(x)是偶函数,所以只需判断x≥0时以上几个方程解的个数即可,而x<0时方程解的个数和x≥0时解的个数相同,最后即可得出满足f[f(x)]=-
的实数x的个数.
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
解答:
解:易知f(x)为偶函数,令f(x)=t,则f[f(x)]=-
变形为f(t)=-
;
t≥0时,f(t)=t2-2t=-
,解得t=1+
,或1-
;
∵f(t)是偶函数;
∴t<0时,f(t)=-
的解为,t=-1-
,或-1+
;
综上得,f(x)=1+
,1-
,-1-
,-1+
;
当x≥0时,
x2-2x=(x-1)2-1=1+
,方程有1解;
x2-2x=(x-1)2-1=1-
,方程有1解;
x2-2x=(x-1)2-1=-1-
,方程无解;
x2-2x=(x-1)2-1=-1+
,方程有2解;
∴当x≥0时,方程f(x)=t有4解;
∵f(x)是偶函数,∴x<0时,f(x)=t也有4解;
综上所述,满足f[f(x)]=-
的实数x的个数为8.
故选D.
| 1 |
| 2 |
| 1 |
| 2 |
t≥0时,f(t)=t2-2t=-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∵f(t)是偶函数;
∴t<0时,f(t)=-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
综上得,f(x)=1+
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当x≥0时,
x2-2x=(x-1)2-1=1+
| ||
| 2 |
x2-2x=(x-1)2-1=1-
| ||
| 2 |
x2-2x=(x-1)2-1=-1-
| ||
| 2 |
x2-2x=(x-1)2-1=-1+
| ||
| 2 |
∴当x≥0时,方程f(x)=t有4解;
∵f(x)是偶函数,∴x<0时,f(x)=t也有4解;
综上所述,满足f[f(x)]=-
| 1 |
| 2 |
故选D.
点评:考查偶函数的概念及偶函数图象的对称性,以及解偶函数方程和判断偶函数方程解的个数所用到的方法:只需求出x≥0时方程的解.

练习册系列答案
相关题目
已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-2),则当x<0时f(x)上的表达式为( )
| A、y=x(x-2) |
| B、y=x(x+2) |
| C、y=-x(x-2) |
| D、y=-x(x+2) |
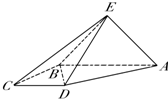 如图,四棱锥E-ABCD中,面ABE⊥面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,且AB∥CD,AB⊥BC,AB=2CD=2BC=2.
如图,四棱锥E-ABCD中,面ABE⊥面ABCD,侧面ABE是等腰直角三角形,EA⊥EB,且AB∥CD,AB⊥BC,AB=2CD=2BC=2.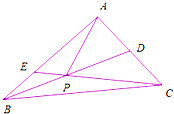 如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若
如图三角形ABC中,AD=DC,AE=2EB,BD与CE相交于点P,若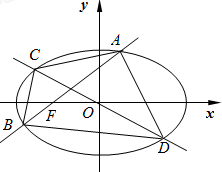 如图,已知椭圆E:
如图,已知椭圆E: