题目内容
 如图所示,在圆心角为90°的扇形AOB中,以圆心O作为起点作射线OC,OD,则使∠AOC+∠BOD<45°的概率为
如图所示,在圆心角为90°的扇形AOB中,以圆心O作为起点作射线OC,OD,则使∠AOC+∠BOD<45°的概率为考点:几何概型
专题:概率与统计
分析:设∠A0C=x,∠BOD=y,建立夹角之间的关系,作出对应的平面区域,利用几何概型的概率公式即可得到结论.
解答:
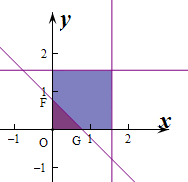 解:设∠A0C=x,∠BOD=y,
解:设∠A0C=x,∠BOD=y,
则0<x<
,0<y<
,
若∠AOC+∠BOD<45°,
即x+y<
,
作出对应的平面区域如图:则F(0,
),G(
,0),
则△oFG的面积S=
×
×
=
,
则正方形的面积S=
×
=
,
则∠AOC+∠BOD<45°的概率为
=
,
故答案为:
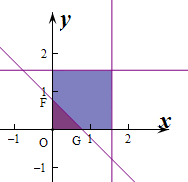 解:设∠A0C=x,∠BOD=y,
解:设∠A0C=x,∠BOD=y,则0<x<
| π |
| 2 |
| π |
| 2 |
若∠AOC+∠BOD<45°,
即x+y<
| π |
| 4 |
作出对应的平面区域如图:则F(0,
| π |
| 4 |
| π |
| 4 |
则△oFG的面积S=
| 1 |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π2 |
| 32 |
则正方形的面积S=
| π |
| 2 |
| π |
| 2 |
| π2 |
| 4 |
则∠AOC+∠BOD<45°的概率为
| ||
|
| 1 |
| 8 |
故答案为:
| 1 |
| 8 |
点评:本题主要考查几何概型的概率公式的计算,列出对应的不等式关系,利用数形结合求出对应的平面区域的面积是解决本题的关键.

练习册系列答案
相关题目
设函数f(x)=
,若函数g(x)=f(x)-k存在两个零点,则实数k的取值范围是( )
|
| A、k<0 | B、0<k<1 |
| C、0<k≤1 | D、k>1 |