题目内容
4.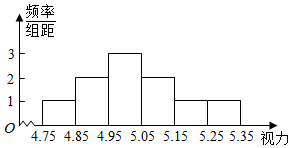 某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064).
某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064).(1)试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况;
(2)求这50名队员视力在5.15以上(含5.15)的人数;
(3)在这50名队员视力在5.15以上(含5.15)的人中任意抽取2人,该2人中视力排名(从高到低)在全省喜爱足球的高中生中前130名的人数记为ξ,求ξ的数学期望.
参考数据:若ξ~N(μ,σ2),则P(μ-σ<ξ≤μ+σ)=0.6826,P(μ-2σ<ξ≤μ+2σ)=0.9544,P(μ-3σ<ξ≤μ+3σ)=0.9974.
分析 (1)用组中值×频率,即可得到结论;
(2)首先理解频数分布直方图横纵轴表示的意义,横轴表示身高,纵轴表示频数,即:每组中包含个体的个数.我们可以依据频数分布直方图,了解数据的分布情况,知道每段所占的比例,从而求出这50名队员视力在5.15以上(含5.15)的人数;
(3)先根据正态分布的规律求出全市前130名的视力在5.25以上,这50人中5.25以上的有2人,确定ξ的可能取值,求出其概率,即可得到ξ的期望.
解答 解:(1)由直方图,经过计算该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况为4.8×0.1+4.9×0.2+5.0×0.3+5.1×0.2+5.2×0.1+5.3×0.1=5.03.…(4分)
(2)由频率分布直方图知,后2组频率为0.2,人数为0.2×50=10,即这50名队员视力在5.15以上(含5.15)的人数为10人.…(6分)
(3)∵P(5.01-3×0.08<ξ≤5.01+3×0.08)=0.9974,
∴P(ξ≥5.25)=0.0013,0.0013×100 000=130.
所以,全市前130名的视力在5.25以上,这50人中5.25以上的有2人.
随机变量ξ可取0,1,2,于是
P(ξ=0)=$\frac{{C}_{8}^{2}}{{C}_{10}^{2}}$=$\frac{28}{45}$,P(ξ=1)=$\frac{{C}_{8}^{1}{C}_{2}^{1}}{{C}_{10}^{2}}$=$\frac{16}{45}$,P(ξ=2)=$\frac{{C}_{2}^{2}}{{C}_{10}^{2}}$=$\frac{1}{45}$,
∴Eξ=0×$\frac{28}{45}$+1×$\frac{16}{45}$+2×$\frac{1}{45}$=$\frac{2}{5}$.…(12分)
点评 此题主要考查了正态分布,考查随机变量的定义及其分布列,并考查了利用分布列求其期望.正确理解频数分布直方图横纵轴表示的意义,由频数分布直方图可以得到什么结论是学习中需要掌握的关键.

| A. | {α|α=k•360°+456°,k∈Z} | B. | {α|α=k•360°+264°,k∈Z} | ||
| C. | {α|α=k•360°+96°,k∈Z} | D. | {α|α=k•360°-264°,k∈Z} |
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
| A. | A⊆B | B. | A?B | C. | B?A | D. | A=B |
| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{1}{2}$ | D. | $\frac{1}{6}$ |