题目内容

15．已知$\overrightarrow{{P}_{1}P}$=-$\frac{2}{3}$$\overrightarrow{P{P}_{2}}$，若实数λ满足$\overrightarrow{P{P}_{2}}$=λ$\overrightarrow{{P}_{2}{P}_{1}}$，则λ的值为-3．

分析 根据向量关系作出平面图形，由线段长度比值可得出答案．

解答 解：∵$\overrightarrow{{P}_{1}P}$=-$\frac{2}{3}$$\overrightarrow{P{P}_{2}}$，∴P，P1，P2三点共线，且P2在线段P1P的反向延长线上，P2P1=$\frac{1}{3}$P2P，

∴$\overrightarrow{P{P}_{2}}$=-3$\overrightarrow{{P}_{2}{P}_{1}}$，
故答案为：-3．

点评 本题考查了平面向量的线性运算，作出图形可快速找到答案．

练习册系列答案
相关题目
1．函数y=$\sqrt{x}$+$\sqrt{2-x}$的最大值为2．
2．已知函数f（x）=x（$\frac{1}{{x}^{2}-1}$+$\frac{1}{2}$）．
（1）求函数f（x）的定义域；
（2）判断函数f（x）的奇偶性并证明你的结论．
3．设m∈R，其中实数x，y满足$\left\{\begin{array}{l}{x≥m}\\{2x-3y+6≥0}\\{3x-2y-6≤0}\end{array}\right.$．若|x+2y|≤18，则实数m的最小值-3．
10．已知定义域为R的奇函数f（x）的周期为4，且x∈（0，2）时f（x）=ln（x2-x+b），若函数f（x）在区间[-2，2]上恰有5个零点，则实数b应满足的条件是（　　）
A．-1＜b≤1B．-1＜b＜1或b=$\frac{5}{4}$C．$\frac{1}{4}$＜b$≤\frac{5}{4}$D．$\frac{1}{4}$＜b≤1或b=$\frac{5}{4}$
20．已知函数f（x）=Asin（x+θ）-cos$\frac{x}{2}$cos（$\frac{π}{6}$-$\frac{x}{2}$）（其中A为常数，θ∈（-π，0），若实数x1，x2，x3满足；①x1＜x2＜x3，②x3-x1＜2π，③f（x1）=f（x2）=f（x3），则θ的值为-$\frac{2π}{3}$．
7．下列各函数在其定义域中，既是奇函数，又是增函数的是（　　）
A．y=x+1B．y=-x3C．y=-$\frac{1}{x}$D．y=x|x|
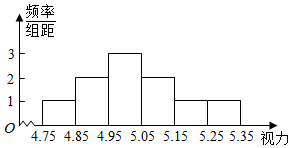4．某市一高中经过层层上报，被国家教育部认定为2015年全国青少年足球特色学校．该校成立了特色足球队，队员来自高中三个年级，人数为50人．视力对踢足球有一定的影响，因而对这50人的视力作一调查．测量这50人的视力（非矫正视力）后发现他们的视力全部介于4.75和5.35之间，将测量结果按如下方式分成6组：第一组[4.75，4.85），第二组[4.85，4.95），…，第6组[5.25，5.35]，如图是按上述分组方法得到的频率分布直方图．又知：该校所在的省中，全省喜爱足球的高中生视力统计调查数据显示：全省100000名喜爱足球的高中生的视力服从正态分布N（5.01，0.0064）．
（1）试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况；
（2）求这50名队员视力在5.15以上（含5.15）的人数；
（3）在这50名队员视力在5.15以上（含5.15）的人中任意抽取2人，该2人中视力排名（从高到低）在全省喜爱足球的高中生中前130名的人数记为ξ，求ξ的数学期望．
参考数据：若ξ～N（μ，σ2），则P（μ-σ＜ξ≤μ+σ）=0.6826，P（μ-2σ＜ξ≤μ+2σ）=0.9544，P（μ-3σ＜ξ≤μ+3σ）=0.9974．
5．若集合A={x|x2-6x+8＜0}，集合B={x∈N|y=$\sqrt{3-x}$}，则A∩B=（　　）
A．{3}B．{1，3}C．{1，2}D．{1，2，3}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网