题目内容
11.已知sin(π-α)-2sin($\frac{π}{2}$+α)=0.(1)求sinαcosα+sin2α的值.
(2)若tan(α+β)=-1,求tanβ的值.
分析 (1)由已知利用诱导公式,同角三角函数基本关系式可求tanα=2,利用同角三角函数基本关系式化简所求即可计算得解.
(2)由tanα=2,利用两角和的正切函数公式即可计算得解.
解答 解:(1)∵sin(π-α)-2sin($\frac{π}{2}$+α)=0,
∴sinα-2cosα=0,可得:tanα=2,
∴sinαcosα+sin2α=$\frac{sinαcosα+si{n}^{2}α}{si{n}^{2}α+co{s}^{2}α}$=$\frac{tanα+ta{n}^{2}α}{ta{n}^{2}α+1}$=$\frac{2+{2}^{2}}{{2}^{2}+1}$=$\frac{6}{5}$.
(2)∵tanα=2,
可得:tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=$\frac{2+tanβ}{1-2tanβ}$=-1,
∴解得:tanβ=3.
点评 本题主要考查了诱导公式,同角三角函数基本关系式,两角和的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
2.已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<\frac{π}{2})$的周期为π,若f(α)=1,则$f(α+\frac{3π}{2})$=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
19.若复数$z=\frac{-2+3i}{i},i$是虚数单位,则z的共轭复数$\overline z$在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
6.任取x、y∈[0,2],则点P(x,y)满足$y≤\frac{1}{x}$的概率为( )
| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{5}{8}$ |
15.已知x,y取值如表:
画散点图分析可知:y与x线性相关,且求得回归方程为$\stackrel{∧}{y}$=x+1,则m的值为$\frac{3}{2}$.
| x | 0 | 1 | 3 | 5 | 6 |
| y | 1 | m | 3m | 5.6 | 7.4 |
17.已知函数f(x)=$\frac{{x}^{2}}{{e}^{x}}$,x≠0,e为自然对数的底数,关于x的方程$\sqrt{f(x)}$+$\frac{2}{\sqrt{f(x)}}$-λ=0有四个相异实根,则实数λ的取值范围是( )
| A. | (0,$\frac{2}{e}$) | B. | (2$\sqrt{2}$,+∞) | C. | (e+$\frac{2}{e}$,+∞) | D. | ($\frac{{e}^{2}}{2}$+$\frac{4}{{e}^{2}}$,+∞) |
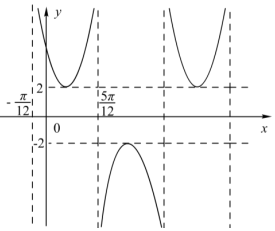 函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.
函数f (x )=$\frac{A}{sin(ωx+φ)}$ ( A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则f($\frac{π}{4}$)=$\frac{4\sqrt{3}}{3}$.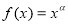 的图象经过点(2,4),则
的图象经过点(2,4),则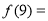 ( )
( )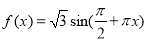 图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数
图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把图象上所有的点向右平移1个单位,得到函数 的图象,则函数
的图象,则函数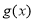 的单调递减区间是( )
的单调递减区间是( )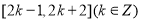 B.
B.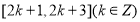
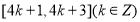 D.
D.