题目内容
19.若复数$z=\frac{-2+3i}{i},i$是虚数单位,则z的共轭复数$\overline z$在复平面内对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 利用复数的运算法则、共轭复数的定义、几何意义即可得出.
解答 解:复数z=$\frac{-i(-2+3i)}{-i•i}$=3+2i,则z的共轭复数$\overline z$=3-2i在复平面内对应的点(3,-2)在第四象限.
故选:D.
点评 本题考查了复数的运算法则、共轭复数的定义、几何意义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
7.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1“是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
4.二次函数y=-x2-4x(x>-2)与指数函数$y={(\frac{1}{2})^x}$的交点个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
6.在等差数列{an}中,a2=14,a5=5,则公差d=( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
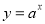 ,②
,② ,③
,③ ,④
,④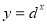 ,根据图象可得a、b、c、d与1的大小关系为( )
,根据图象可得a、b、c、d与1的大小关系为( )
 万件与每台机器的日产量
万件与每台机器的日产量 万件
万件 之间满足关系:
之间满足关系: .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.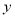 表示为
表示为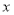 的函数;
的函数;