题目内容
15.已知x,y取值如表:| x | 0 | 1 | 3 | 5 | 6 |
| y | 1 | m | 3m | 5.6 | 7.4 |
分析 计算$\overline{x}$、$\overline{y}$,根据线性回归方程过样本中心点,代入方程求出m的值.
解答 解:计算$\overline{x}$=$\frac{1}{5}$×(0+1+3+5+6)=3,
$\overline{y}$=$\frac{1}{5}$×(1+m+3m+5.6+7.4)=$\frac{14+4m}{5}$,
∴这组数据的样本中心点是(3,$\frac{14+4m}{5}$),
又y与x的线性回归方程$\stackrel{∧}{y}$=x+1过样本中心点,
∴$\frac{14+4m}{5}$=1×3+1,
解得m=$\frac{3}{2}$,
即m的值为$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 本题考查了回归直线方程过样本中心点的应用问题,是基础题目.

练习册系列答案
相关题目
7.已知命题p:对任意x∈R,总有2x>x2;q:“ab>1“是“a>1,b>1”的充分不必要条件,则下列命题为真命题的是( )
| A. | p∧q | B. | ¬p∧q | C. | p∧¬q | D. | ¬p∧¬q |
4.二次函数y=-x2-4x(x>-2)与指数函数$y={(\frac{1}{2})^x}$的交点个数有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
20.已知向量$\overrightarrow{BA}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$),$\overrightarrow{BC}$=(0,1),则向量$\overrightarrow{BA}$与$\overrightarrow{BC}$夹角的大小为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
6.在等差数列{an}中,a2=14,a5=5,则公差d=( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
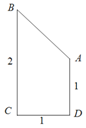 如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$.
如图,直角梯形ABCD中,AD⊥DC,AD∥BC,BC=2CD=2AD=2,若将直角梯形绕BC边旋转一周,则所得几何体的表面积为$(3+{\sqrt{2}^{\;}})π$. ,若其定义域内不存在实数
,若其定义域内不存在实数 ,使得
,使得 ,则
,则 的取值范围是_____.
的取值范围是_____.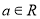 ,则“
,则“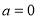 ”是“
”是“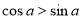 ”的( )
”的( )