题目内容
17.已知函数f(x)=$\frac{{x}^{2}}{{e}^{x}}$,x≠0,e为自然对数的底数,关于x的方程$\sqrt{f(x)}$+$\frac{2}{\sqrt{f(x)}}$-λ=0有四个相异实根,则实数λ的取值范围是( )| A. | (0,$\frac{2}{e}$) | B. | (2$\sqrt{2}$,+∞) | C. | (e+$\frac{2}{e}$,+∞) | D. | ($\frac{{e}^{2}}{2}$+$\frac{4}{{e}^{2}}$,+∞) |
分析 求导数,确定函数的单调性,可得x=2时,函数取得极大值$\frac{4}{{e}^{2}}$,关于x的方程$\sqrt{f(x)}$+$\frac{2}{\sqrt{f(x)}}$-λ=0有四个相异实根,则t+$\frac{2}{t}$-λ=0的一根在(0,$\frac{2}{e}$),另一根在($\frac{2}{e}$,+∞)之间,即可得出结论.
解答 解:由题意,f′(x)=$\frac{x(2-x)}{{e}^{x}}$,
∴x<0或x>2时,f′(x)<0,函数单调递减,0<x<2时,f′(x)>0,函数单调递增,
∴x=2时,函数取得极大值$\frac{4}{{e}^{2}}$,
关于x的方程$\sqrt{f(x)}$+$\frac{2}{\sqrt{f(x)}}$-λ=0有四个相异实根,则t+$\frac{2}{t}$-λ=0的一根在(0,$\frac{2}{e}$),另一根在($\frac{2}{e}$,+∞)之间,
∴$\frac{2}{e}+e-λ<0$,∴λ>e+$\frac{2}{e}$,
故选:C.
点评 本题考查函数的单调性,考查方程根问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.在等差数列{an}中,a2=14,a5=5,则公差d=( )
| A. | -2 | B. | -3 | C. | 2 | D. | 3 |
 ,若其定义域内不存在实数
,若其定义域内不存在实数 ,使得
,使得 ,则
,则 的取值范围是_____.
的取值范围是_____.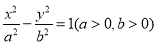 的左、右焦点分别为
的左、右焦点分别为 ,
, ,以
,以 为圆心,
为圆心, 为半径的圆与双曲线在第一、二象限内依次交于
为半径的圆与双曲线在第一、二象限内依次交于 ,
, 两点,若
两点,若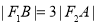 ,则该双曲线的离心率是( )
,则该双曲线的离心率是( )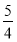 B.
B.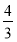 C.
C. D.2
D.2  万件与每台机器的日产量
万件与每台机器的日产量 万件
万件 之间满足关系:
之间满足关系: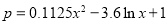 .已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.
.已知每生产1万件合格的产品可以以盈利3万元,但每生产1万件次品将亏损1万元.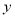 表示为
表示为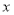 的函数;
的函数;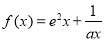 (
(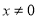 ,
, )在
)在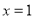 处的切线与直线
处的切线与直线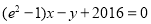 平行.
平行.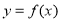 的单调性;
的单调性;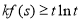 在
在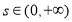 ,
,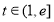 上恒成立,求实数
上恒成立,求实数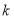 的取值范围.
的取值范围.