题目内容
12.对于每个实数x,设f(x)取$y=2\sqrt{x}$,y=|x-2|两个函数中的较小值.若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1、x2、x3,则x1+x2+x3的取值范围是( )| A. | (2,$6-2\sqrt{3}$) | B. | (2,$\sqrt{3}+1$) | C. | (4,$8-2\sqrt{3}$) | D. | (0,$4-2\sqrt{3}$) |
分析 根据函数f(x)的定义作出函数f(x)的图象,根据函数图象有三个交点,确定三个交点之间的关系即可得到结论.
解答 解:由2$\sqrt{x}$=|x-2|,
平方得4x=x2-4x+4,
即x2-8x+4=0,
解得x=4+2$\sqrt{3}$或x=4-2$\sqrt{3}$,
设x1<x2<x3,
作出函数f(x)的图象如图:
则0<x1<4-2$\sqrt{3}$,x2与x3,关于x=2对称,
则x2+x3=4,
则x1+x2+x3=x1+4,
∵0<x1<4-2$\sqrt{3}$,
∴4<4+x1<8-2$\sqrt{3}$,
即x1+x2+x3的取值范围为(4,8-2 $\sqrt{3}$),
故选:C
点评 本题主要考查函数与方程的应用,根据定义作出函数的图象,结合函数的对称性是解决本题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
20.我国古代数学名著《九章算术》中有如下问题:今有甲乙丙三人持钱,甲语乙丙:各将公等所持钱,半以益我,钱成九十(意思是把你们两个手上的钱各分我一半,我手上就有90钱);乙复语甲丙,各将公等所持钱,半以益我,钱成七十;丙复语甲乙:各将公等所持钱,半以益我,钱成五十六,则乙手上有( )钱.
| A. | 28 | B. | 32 | C. | 56 | D. | 70 |
1.等差数列{an}的前n项和为sn,若a2+a3=5,S5=20,则a5=( )
| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
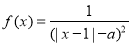 的定义域为
的定义域为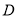 ,其中
,其中 .
.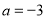 时,写出函数
时,写出函数 的单调区间(不要求证明);
的单调区间(不要求证明);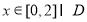 ,均有
,均有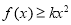 成立,求实数
成立,求实数 的取值范围.
的取值范围.