题目内容
4.已知A为双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)的右顶点,B1,B2分别为虚轴的两个端点,F为右焦点.若B2F⊥AB1,则双曲线C的离心率是$\frac{\sqrt{5}+1}{2}$.分析 双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)可得A、F、B1和B2各点的坐标,B2F⊥AB1,利用向量数量积的坐标公式得到ac-b2=0,结合b2=c2-a2和离心率公式,化简得离心率e的方程,即可解出该双曲线的离心率.
解答 解:由题意,双曲线C:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1(a>0,b>0)可得A(a,0),F(c,0),B1(0,b),B2(0,-b)
∵$\overrightarrow{A{B}_{1}}$=(-a,b),$\overrightarrow{{B}_{2}F}$=(c,b)
∴由$\overrightarrow{A{B}_{1}}$⊥$\overrightarrow{{B}_{2}F}$得$\overrightarrow{A{B}_{1}}$•$\overrightarrow{{B}_{2}F}$=0,即-ac+b2=0
可得b2=ac,即c2-ac-a2=0,两边都除以a2可得e2-e-1=0
解之得e=$\frac{\sqrt{5}+1}{2}$(舍负)
故答案为:$\frac{\sqrt{5}+1}{2}$.
点评 本题给出双曲线方程,在已知向量垂直的情况下求离心率.着重考查了平面向量数量积公式和双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案
相关题目
15.已知x,y∈(0,+∞),且满足$\frac{1}{x}+\frac{1}{2y}=2$,那么x+4y的最小值为( )
| A. | $\frac{3}{2}-\sqrt{2}$ | B. | $3+\frac{{\sqrt{2}}}{2}$ | C. | $\frac{3}{2}+\sqrt{2}$ | D. | $3-\frac{{\sqrt{2}}}{2}$ |
12.对于每个实数x,设f(x)取$y=2\sqrt{x}$,y=|x-2|两个函数中的较小值.若动直线y=m与函数y=f(x)的图象有三个不同的交点,它们的横坐标分别为x1、x2、x3,则x1+x2+x3的取值范围是( )
| A. | (2,$6-2\sqrt{3}$) | B. | (2,$\sqrt{3}+1$) | C. | (4,$8-2\sqrt{3}$) | D. | (0,$4-2\sqrt{3}$) |
9.运行如图的程序框图,如果输出的数是13,那么输入的正整数n的值是( )


| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
12.若x,y满足约束条件$\left\{\begin{array}{l}y≤x\\ x+y≤1\\ y≥-1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | 5 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |

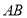 为圆锥
为圆锥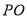 的底面直径,
的底面直径,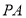 为母线,点
为母线,点 在底面圆周上,若
在底面圆周上,若 ,
,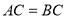 ,则二面角
,则二面角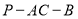 大小的正切值是( )
大小的正切值是( )
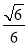 B.
B. C.
C.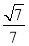 D.
D.