题目内容
已知直线AB和CD是异面直线,AB∥α,CD∥α,AC∩α=M,BD∩α=N,求证:
=
.
| AM |
| MC |
| BN |
| ND |
考点:空间中直线与直线之间的位置关系
专题:空间位置关系与距离
分析:过点A作AE⊥α于E,过点C作CF⊥α于F,则AE是AB到平面α的距离,CF是CD到平面α的距离,由已知推导出
=
=
,
=
,由此能证明
=
.
| AM |
| MC |
| AE |
| CF |
| AB到平面α的距离 |
| CD到平面α的距离 |
| BN |
| ND |
| AB到平面α的距离 |
| CD到平面α的距离 |
| AM |
| MC |
| BN |
| ND |
解答:
解:过点A作AE⊥α于E,过点C作CF⊥α于F,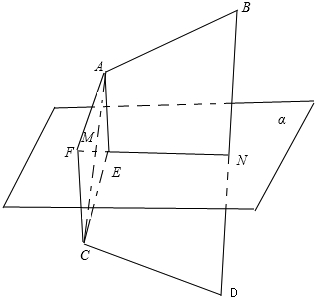
显然,AE是AB到平面α的距离,
CF是CD到平面α的距离,
且有:AE∥CF,
∴A、E、C、F 四点在同一平面内,
点M在AC上,那么也在平面AECF上,
在平面AECF内,∵AE∥CF,且AC和EF相交于点M,
∴△AEM∽△CFM,
∴
=
=
,
同理,得:
=
,
∴
=
.

显然,AE是AB到平面α的距离,
CF是CD到平面α的距离,
且有:AE∥CF,
∴A、E、C、F 四点在同一平面内,
点M在AC上,那么也在平面AECF上,
在平面AECF内,∵AE∥CF,且AC和EF相交于点M,
∴△AEM∽△CFM,
∴
| AM |
| MC |
| AE |
| CF |
| AB到平面α的距离 |
| CD到平面α的距离 |
同理,得:
| BN |
| ND |
| AB到平面α的距离 |
| CD到平面α的距离 |
∴
| AM |
| MC |
| BN |
| ND |
点评:本题考查两线段比值相等的证明,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
若z=
,则z的共轭复数的虚部为( )
| 1+2i |
| i |
| A、i | B、-i | C、1 | D、-1 |
直线a?平面α,直线b?平面α,M∈a,N∈b,且M∈l,N∈l,则( )
| A、l?α | B、l?α |
| C、l∩α=M | D、l∩α=N |
下列等式中不正确的是( )
A、n!=
| ||||
B、
| ||||
C、
| ||||
D、
|
三名学生到高一年级的四个班就读,每个班至多进一名学生,则不同的进班方式有( )
| A、4种 | ||
B、
| ||
| C、34种 | ||
| D、43种 |