题目内容
设二次函数图象为f（x）=x2+ax+a-2的图象与x轴有两个交点，且两个交点之间距离为2
，求a的值．
| 5 |
考点：二次函数的性质
专题：计算题,函数的性质及应用
分析：由题意，设交点为A（m，0），B（n，0），则m，n是方程x2+ax+a-2=0的两个不同的根，利用韦达定理求解．
解答：
解：由题意，设交点为A（m，0），B（n，0），
则m，n是方程x2+ax+a-2=0的两个不同的根，
故△=a2-4（a-2）=（a-2）2+4＞0，
m+n=-a，mn=a-2，
则（m-n）2=（m+n）2-4nm=（a-2）2+4=20，
解得a=6或a=-2．
则m，n是方程x2+ax+a-2=0的两个不同的根，
故△=a2-4（a-2）=（a-2）2+4＞0，
m+n=-a，mn=a-2，
则（m-n）2=（m+n）2-4nm=（a-2）2+4=20，
解得a=6或a=-2．
点评：本题考查了二次函数与二次方程的性质，属于基础题．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
若（
）x=8．则log27x2=（ ）
| 1 |
| 2 |
| A、2 | ||
B、-
| ||
C、
| ||
D、
|
设
=
（
+5
），
=-2
+8
，
=3（
-
），则共线的三点是（ ）
| AB |
| ||
| 2 |
| a |
| b |
| BC |
| a |
| b |
| CD |
| a |
| b |
| A、A，B，C |
| B、B，C，D |
| C、A，B，D |
| D、A，C，D |
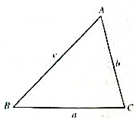如图所示，△ABC的三边分别为a、b、c．