题目内容
| 1+2i |
| 1+i |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
考点:复数代数形式的乘除运算
专题:数系的扩充和复数
分析:分子分母同乘以分的共轭复数1-i,化简即可.
解答:
解:化简可得
=
=
=
=
+
i
故选:C
| 1+2i |
| 1+i |
| (1+2i)(1-i) |
| (1+i)(1-i) |
=
| 1-i+2i-2i2 |
| 1-i2 |
| 3+i |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
故选:C
点评:本题考查复数的代数形式的乘除运算,属基础题.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
阅读如图程序:

如果输入x=-2,则输出结果y为( )

如果输入x=-2,则输出结果y为( )
| A、π-5 | B、-π-5 |
| C、3+π | D、3-π |
若a=20.5,b=logπ3,c=log
e,则( )
| 1 |
| 2 |
| A、a>b>c |
| B、b>a>c |
| C、c>a>b |
| D、b>c>a |
当x∈(0,
)时,下面四个函数中最大的是( )
| π |
| 4 |
| A、sin(cosx) |
| B、sin(sinx) |
| C、cos(sinx) |
| D、cos(cosx) |
若向量
≠
,|
|=1,对任意的t∈R,|
-t
|≥|
-
|成立,则
•
=( )
| a |
| e |
| e |
| a |
| e |
| a |
| e |
| a |
| e |
| A、0 | ||
| B、1 | ||
| C、-1 | ||
D、
|
若函数f(x)=2sin(ωx+φ)的部分图象如图所示,则ω和φ的取值是( )
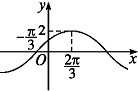

A、ω=
| ||||
B、ω=
| ||||
C、ω=1,φ=-
| ||||
D、ω=1,φ=
|