题目内容
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x-y+3=0平行,若数列{
}的前n项和为S2015的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:利用导数研究曲线上某点切线方程,二次函数的性质,数列的求和
专题:函数的性质及应用,点列、递归数列与数学归纳法
分析:根据导数的定义求出函数f(x)的解析式,然后求出数列的通项公式,从而得到答案.
解答:
由题可知函数f(x)的图象在点A处的切线l的斜率为1,
又f′(x)=2x+2b,故f′(0)=2b=1,
即b=
,从而f(x)=x2+x.
故
=
-
.
所以S2015=(1-
)+(
-
)+…(
-
)+(
-
)=
.
故选:D.
又f′(x)=2x+2b,故f′(0)=2b=1,
即b=
| 1 |
| 2 |
故
| 1 |
| f(x) |
| 1 |
| x |
| 1 |
| x+1 |
所以S2015=(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2014 |
| 1 |
| 2015 |
| 1 |
| 2015 |
| 1 |
| 2016 |
| 2015 |
| 2016 |
故选:D.
点评:本题主要考察导数的意义及数列的前n项和求法.

练习册系列答案
相关题目
函数y=log
(x2-3x+2)的单调递增区间为( )
| 1 |
| 2 |
| A、(-∞,1) | ||
B、(-∞,
| ||
C、[
| ||
| D、(2,+∞) |
 如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为( )
如图所示,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是等腰梯形,等腰直角三角形和长方形,则该几何体表面积为( )| A、14 | ||
B、14+2
| ||
C、8+8
| ||
| D、16 |
 如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.
如图,四边形ABCD为菱形,ACFE为平行四边形,且平面ACFE⊥平面ABCD,设BD与AC相交于点G,H为FG的中点.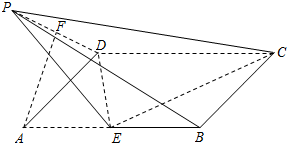 如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.
如图所示,在矩形ABCD中,AD=1,AB=2,点E是线段AB的中点,把三角形AED沿DE折起,设折起后点A的位置为 P,F是PD的中点.