题目内容
已知{an}是首项为17,公差为-2的等差数列,Sn为{an}的前n项和.
(1)求数列{an}的通项公式及前n项和Sn;
(2)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及前n项和Tn.
(1)求数列{an}的通项公式及前n项和Sn;
(2)设{bn-an}是首项为1,公比为3的等比数列,求数列{bn}的通项公式及前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)利用等差数列的通项公式及其前n项和公式即可得出.
(2)利用等差数列与等比数列的前n项和公式及其公式12+22+32+…+n2=
即可得出.
(2)利用等差数列与等比数列的前n项和公式及其公式12+22+32+…+n2=
| n(n+1)(2n+1) |
| 6 |
解答:
解:(1)∵{an}是首项为17,公差为-2的等差数列,
∴an=17-2(n-1)=19-2n,
∴Sn=
=-n2+18n.
(2)∵{bn-an}是首项为1,公比为3的等比数列,
∴bn-an=3n-1,
∴bn=an+3n-1=-n2+18n+3n-1,
∴Tn=-
+18×
+
=-
+9n2+9n+
×3n-
.
∴an=17-2(n-1)=19-2n,
∴Sn=
| n(17+19-2n) |
| 2 |
(2)∵{bn-an}是首项为1,公比为3的等比数列,
∴bn-an=3n-1,
∴bn=an+3n-1=-n2+18n+3n-1,
∴Tn=-
| n(n+1)(2n+1) |
| 6 |
| n(n+1) |
| 2 |
| 3n-1 |
| 3-1 |
=-
| n(n+1)(2n+1) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了等差数列与等比数列的前n项和公式及其公式12+22+32+…+n2=
,考查了推理能力与计算能力,属于中档题.
| n(n+1)(2n+1) |
| 6 |

练习册系列答案
相关题目
已知函数f(x)=x2+2bx的图象在点A(0,f(0))处的切线l与直线x-y+3=0平行,若数列{
}的前n项和为S2015的值为( )
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|
若a=
xdx,b=
dx,c=
2dx,则a,b,c的大小关系为( )
| ∫ | 4 2 |
| ∫ | 4 2 |
| 4 |
| x |
| ∫ | 4 2 |
| A、a<b<c |
| B、b<a<c |
| C、b<c<a |
| D、c<b<a |
已知函数f(x)是定义在[-1,1]上的奇函数,对于任意x1,x2∈[-1,1],x1≠x2,总有
>0且f(1)=1.若对于任意α∈[-1,1],使f(x)≤t2-2αt-1成立,则实数t的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| A、-2≤t≤2 | ||||
B、t≤-1-
| ||||
| C、t≤0或t≥2 | ||||
| D、t≥2或t≤-2或t=0 |

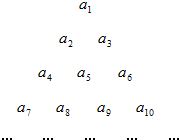 已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=
已知数列{an}中,a1=2,a5=10,an+2=2an+1-an(n∈N*),把数列{an}的各项排成如图所示的三角形状,记F(m,n)表示第m行、第n列的项,若F(m,n)+F(m+1,n+1)=90,则m+n=