题目内容

计算：∫xexdx=
 
．
考点：定积分
专题：导数的综合应用
分析：根据不定积分的公式即可得到结论．
解答： 解：由分步积分公式有
∫xexdx=∫xd（ex）=x•ex-∫exdx=xex-ex+c．
故答案为：xex-ex+c
点评：本题主要考查不定积分的计算，要求熟练掌握分步积分的运算公式，比较基础．
练习册系列答案
相关题目
试比较log23.4、log43.6、log3
10
3
的大小．
求二项式（a+b）n的展开式．
公比q不为1的等比数列{an}满足an+2+an+1=2an(n∈N*)，则q=
 
．
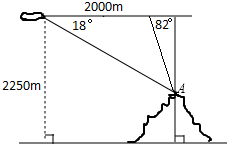如图，一只气球在2250m的高空水平飞行，气球上的工作人员测得前方一座山顶上A点处的俯角为18°，当气球向前飞行了2000m后，又测得前方A点处的俯角为82°，则山的高度为
 
（精确到1m）
若存在x∈[2，+∞），使不等式
1+ax
x•2x
≥1成立，则实数a的最小值为
 
．
已知抛物线C：x2=4y与点M（
3
2
，-1），过C的焦点且斜率为k的直线与C交于A，B两点，若
MA
•
MB
=0，则直线AB与抛物线C围成的面积为
 
．
用符号[x）表示超过x的最小整数，如[π）=4，[-1.5）=-1，记{x}=[x）-x．
（1）若x∈（1，2），则不等式{x}•[x）＜x的解集为
 
；
（2）若x∈（1，3），则方程cos2[x）+sin2{x}-1=0的实数解为
 
．
给出下列四个命题，其错误的是
①已知q是等比数列{an}的公比，则“数列{an}是递增数列”是“q＞1”的既不充分也不必要条件．
②若定义在R上的函数y=f（x）是奇函数，则对定义域内的任意x必有f（2x+1）+f（-2x-1）=0．
③若存在正常数p满足f(px)=f(px+
p
2
)，则f（x）的一个正周期为
p
2
．
④函数y=f（x+1）与y=f（1-x）图象关于x=1对称．（　　）
A、②④B、④C、③D、③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网