题目内容
已知函数f（x）=2sin（ωx），其中常数ω＞0，令ω=2，将函数y=f（x）的图象向左平移个
单位，再向上平移1个单位，得到函数y=g（x）的图象，若函数y=g（z）在区间[m，m+10π]（-
＜m＜
）上有20个零点：a1，a2，a3，…，a20，求a1+a2+a3+…+a20的值．
| π |
| 6 |
| π |
| 4 |
| 5π |
| 12 |
考点：函数y=Asin（ωx+φ）的图象变换,数列的求和
专题：三角函数的图像与性质
分析：根据图象平移变换求出g（x），令g（z）=0，求得z=kπ+
，或 z=kπ+
，k∈z，可得 a1+a2+a3+…+a19+a20=[
+（π+
）+（2π+
）+…+（9π+
）]+[
+（π+
）+（2π+
）+…+（9π+
）]，计算求得结果．
| 5π |
| 12 |
| 3π |
| 4 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
解答：
解：由题意可得，g（x）=2sin2（x+
）+1=2sin（2x+
）+1．
若函数y=g（x）在区间[m，m+10π]上有20个零点，则区间[m，m+10π]恰好包含10个周期，
函数在区间[m+kπ，m+（k+1）π]上恰有两个零点，故在[m，m+10π]上有20个零点．
令g（z）=2sin（2z+
）+1=0，求得 sin（2z+
）=-
，
∴2z+
=2kπ+
，或2z+
=2kπ+
，即 z=kπ+
，或 z=kπ+
，k∈z．
再结合-
＜m＜
，在区间[m，m+10π]上，∴a1+a2+a3+…+a19+a20
=[
+（π+
）+（2π+
）+…+（9π+
）]+[
+（π+
）+（2π+
）+…+（9π+
）]
=
+
=
．
| π |
| 6 |
| π |
| 3 |
若函数y=g（x）在区间[m，m+10π]上有20个零点，则区间[m，m+10π]恰好包含10个周期，
函数在区间[m+kπ，m+（k+1）π]上恰有两个零点，故在[m，m+10π]上有20个零点．
令g（z）=2sin（2z+
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
∴2z+
| π |
| 3 |
| 7π |
| 6 |
| π |
| 3 |
| 11π |
| 6 |
| 5π |
| 12 |
| 3π |
| 4 |
再结合-
| π |
| 4 |
| 5π |
| 12 |
=[
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 5π |
| 12 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
=
| 295 |
| 6 |
| 105π |
| 2 |
| 305 |
| 3 |
点评：本题考查函数y=Asin（ωx+φ）的图象变换、函数的奇偶性、根的存在性及根的个数的判断，考查数形结合思想，结合图象分析是解决问题的关键，属于基础题．
练习册系列答案
相关题目
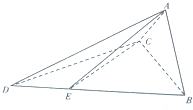如图，四面体A-BCD中，平面ABC⊥平面BCD，AC=AB，CB=CD，∠DCB=120°．点E在BD上，且DE=