题目内容
某班甲、乙两名学同参加100米达标训练,在相同条件下两人10次训练的成绩(单位:秒)如下:
(1)从甲、乙两人的10次训练成绩中各随机抽取一次,求抽取的成绩中至少有一个比12.8秒差的概率.
(2)后来经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 甲 | 11.6 | 12.2 | 13.2 | 13.9 | 14.0 | 11.5 | 13.1 | 14.5 | 11.7 | 14.3 |
| 乙 | 12.3 | 13.3 | 14.3 | 11.7 | 12.0 | 12.8 | 13.2 | 13.8 | 14.1 | 12.5 |
(2)后来经过对甲、乙两位同学的多次成绩的统计,甲、乙的成绩都均匀分布在[11.5,14.5]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.8秒的概率.
考点:几何概型
专题:计算题,概率与统计
分析:(1)设事件A为:甲的成绩低于12.8,事件B为:乙的成绩低于12.8,我们先计算出从甲、乙成绩都低于12.8的概率,再利用对立事件概率公式即可求出答案.
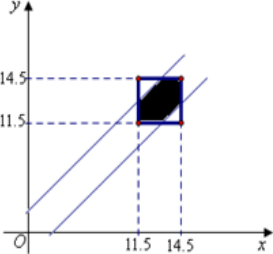
(2)设甲、乙的成绩分别为x,y,则|x-y|<0.8,如图阴影部分面积我们可以求出它所表示的平面区域的面积,再求出甲、乙成绩之差的绝对值小于0.8分对应的平面区域的面积,代入几何概型公式,即可得到答案.
(2)设甲、乙的成绩分别为x,y,则|x-y|<0.8,如图阴影部分面积我们可以求出它所表示的平面区域的面积,再求出甲、乙成绩之差的绝对值小于0.8分对应的平面区域的面积,代入几何概型公式,即可得到答案.
解答:
解:(1)甲的10次训练成绩中不比12.8秒差的有4次;乙的10次训练成绩中不比12.8秒差的有5次,
∴抽取的两次成绩中都不比12.8秒差的概率为
×
=
,
∴其对立事件抽取的成绩中至少有一个比12.8秒差的概率为1-
=
;
(2)甲、乙的成绩分别为x,y,则满足条件甲、乙成绩之差的绝对值小于0.8秒,即|x-y|<0.8的平面区域为图中阴影部分,
∴甲、乙成绩之差的绝对值小于0.8秒的概率P=
=
.
∴抽取的两次成绩中都不比12.8秒差的概率为
| 4 |
| 10 |
| 5 |
| 10 |
| 1 |
| 5 |
∴其对立事件抽取的成绩中至少有一个比12.8秒差的概率为1-
| 1 |
| 5 |
| 4 |
| 5 |
(2)甲、乙的成绩分别为x,y,则满足条件甲、乙成绩之差的绝对值小于0.8秒,即|x-y|<0.8的平面区域为图中阴影部分,
∴甲、乙成绩之差的绝对值小于0.8秒的概率P=
| 3×3-2.2×2.2 |
| 3×3 |
| 104 |
| 225 |

点评:本题考查了古典概型的概率计算及对立事件概率公式,考查了几何概型的概率计算,熟练掌握几何概型的概率求法及对立事件概率公式是解题的关键.

练习册系列答案
相关题目
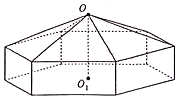 一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积.
一个帐篷的下部形状是高为1m的正六棱柱,上部的形状是侧棱长为3m的正六棱锥(图).帐篷的顶点O到底面中心O1的距离为2m,求帐篷的体积. 某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了100名学生的成绩,得到如图所示的成绩频率分布直方图.
某市的教育研究机构对全市高三学生进行综合素质测试,随机抽取了100名学生的成绩,得到如图所示的成绩频率分布直方图.